Sześciokąt foremny. A.B.C.D: zad1. Sześciokąt foremny o boku 4 cm podzielono przekątnymi wychodzącymi z jednego wierzchołka na cztery trójkąty. a. Wszystkie otrzymane trójkąty są przystające b. wszystkie otrzymane trójkąty są podobne c. dwa spośród tych trójkątów mają pole równe 16 pierw z 3 cm kwadratowych d. dwa spośród tych trójkątów mają obwód równy 4(3+ pierw z 3)cm Bardzo proszę o rysunek i wyjaśnienie.

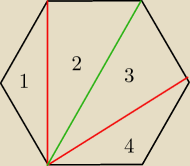
ICSP: bok = 4 czerwony = krótsza przekątna = 4√3 zielony = dłuższa przekątna = 8 teraz dopasuj odp . P.S. Trójkąty są oznaczone cyferkami

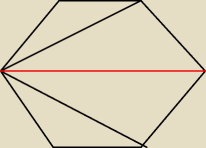
loitzl9006: widać zatem że odpowiedzi a i b od razu odpadają a co do odpowiedzi c i d to wykorzystaj fakt, że dłuższa (czerwona) przekątna sześciokąta jest dwa razy dłuższa od jego boku. Wynika to z tego że sześciokąt foremny o boku długości a dzieli się na sześć trójkątów równobocznych o boku długości a

loitzl9006: ICSP ładniej się postarałeś

ICSP: Nie ma się co starać Przecież w panelu rysowania masz sześciokąt foremny

loitzl9006: o kurde faktycznie oświeciłeś mnie

A.B.C.D: Chyba już rozumiem Czyli krótszą przekątna mogę obliczyć z twierdzenia Pitagorasa?

loitzl9006: tak

A.B.C.D: Czy to będzie odpowiedź d?

loitzl9006: zgadza się

A.B.C.D: Dziękuję bardzo !

sylwia: a czy czerwona przekątna nie bedzie miała przypadkiem 4 pierwiastek z 2, bo to przeciwprostokątna trójkąta równoramiennego ma przecież: a pierwiastek z dwóch

sylwia: a nie sorry to gdy trójkąt jest prostokątny, nie zauważyłam moj bład