. melania.: w trojkacie prostokatnym przyprostokatne maja dlugosc 12 cm i 5 cm. przez wierzcholek kata prostego poprowadzono prosta, ktora podzielilaten trojkat na dwa trojkaty o rownych obwodach. oblicz stosunek dlugosci promieni okregow wpisanych w powstale trojkaty. bardzo bym prosila o wytlumaczenie, co, jak , skad.

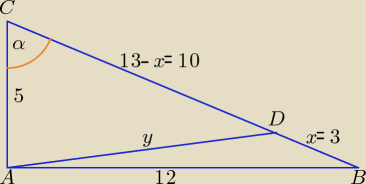
Bogdan: Wskazówki: |BC| = √25 + 144 = 13 5 + y + 13 − x = 12 + y + x ⇒ 2x = 6 ⇒ x = 3 Z twierdzenia kosinusów w trójkącie ADC:

	5
y2 = 25 + 100 − 2*5*10*cosα, cosα =
	13

	5
y2 = 125 − 100*
	13

Stąd obliczamy y. r₁ − długość promienia okręgu wpisanego w trójkąt ADC, r₂ − długość promienia okręgu wpisanego w trójkąt ABD,

	1
p1 =		(5 + 10 + y),
	2

	1
p2 =		(12 + 3 + y),
	2

P₁ − pole trójkąta ADC, P₂ − pole trójkąta ABD.

	P1		P2
r1 =		, r2 =
	p1		p2

modliszka: