Zbadaj liczbe pierwiastkow rownania w zaleznosci od wartosci parametru m Mati00721: Zbadaj liczbe pierwiastkow rownania w zaleznosci od wartosci parametru m: x²−3|x|−4=m

Saizou : narysuje funkcję f(x)=x²−3lxl−4 i odczytaj liczbę rozwiązań

Mati00721: ale chodzi mi o to, jak mam tą wartosc bezwzgledna narysowac

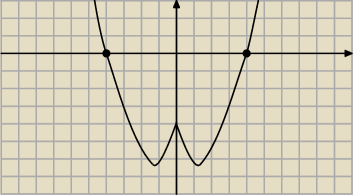
Saizou : I dla x≥0 h(x)=x²−3x−4 II dla x<0 g(x)x²+3x−4 zatem otrzymamy<patrz rysunek>

Mati00721: ok dzieki

Saizou : albo I dla x≥0 h(x)=x²−3x−4 mamy obliczyć miejsca zerowe funkcji zatem 0=x²−3x−4 x₁=4 x₂=−1 sprzeczność nie spełnia założenia x≥0 II dla x<0 g(x)=x²+3x−4 x₁=−4 x₂=1 sprzeczność nie spełnia założenia x<0 zatem ostatecznie f(x)=0⇔x∊{−4:4}

Mila: Saizou, Mati odpowiedź? ( liczba rozwiązań) Trzeba jeszcze obliczyć współrzędne wierzchołka paraboli i podać punkt przecięcia osi OY.

Aga1.:

	−Δ
Potrzebna jest jeszcze druga współrzędna wierzchołka yw=		=
	4a

i punkt wspólny z osią OY : (0−4) Odp. Dla m<y_w równanie nie ma rozwiązania Dla m∊{y_w}U(−4,∞) równanie ma 2 rozwiązania Dla m=−4 równanie ma 3 rozwiązania Dla m∊(y_w,−4) równanie ma 4 rozwiązania

Saizou : wiedziałem że coś źle robię, tylko nie wiedziałem co no nic pozostaje tylko przeprosić za wprowadzenie w błąd

Mila: Saizou, zadanie było niedokończone. Rysunek bardzo dobry i potrzebny.