wartość bezwzględna tech: Wyznacz zbiór wartości funkcji f(x)= |x−1| + |x+4| Jak za to się zabrać? Czy trzeba robić na kilka przypadków?

Artur z miasta Neptuna: mozna mozna też narysować tą funkcję

Bogdan: Dla x∊(−∞, −4): f(x) = −(x − 1) − (x + 4) ⇒ f(x) = ... Dla x∊<−4, 1): f(x) = −(x − 1) + (x + 4) ⇒ f(x) = ... Dla x∊<1, +∞): f(x) = (x − 1) + (x + 4) ⇒ f(x) = ...

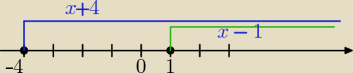
Mila: 1) zaznaczam na osi liczbowej przedziały: dla x−1≥0⇔x≥1 dla x+4≥0⇔x≥−4 2) f(x)=|x−1|+|x+4| ustalamy wzór w każdym z przedziałów a) x<−4 to f(x)=−x+1−x−4⇔f(x)=−2x−4 b) x≥−4 i x<1 to f(x)=−x+1+ x+4 ⇔ f(x)=5 c) x≥1 to f(x)= x−1+x+4 ⇔f(x)=2x+3 3) rysujesz wykres funkcji

tech: Dla x∊(−∞, −4): f(x) = −(x − 1) − (x + 4) ⇒ f(x) = −2x − 3 Dla x∊<−4, 1): f(x) = −(x − 1) + (x + 4) ⇒ f(x) = 5 Dla x∊<1, +∞): f(x) = (x − 1) + (x + 4) ⇒ f(x) = 2x + 3 czyli będzie f(D_f): y∊<5;+≈> zgadza się?

tech: pomyliłem się: f(D_f): y∊<5;+≈)

Mila: Ja się pomyliłam w sumowaniu: a) f(x)= −2x−3 Zw=<5;∞)

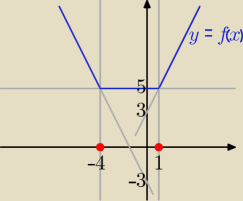
Bogdan: Dla x∊(−∞, −4): f(x) = −2x − 3 Dla x∊<−4, 1): f(x) = 5 Dla x∊<1, +∞): f(x) = 2x + 3

Gustlik: Metoda "osi i tabelki" − https://matematykaszkolna.pl/forum/forum.py?komentarzdo=1796 . Podobna do metody Bogdana, tylko w tabelce rozpisuję, gdzie wyrażenia zmieniają znak, a gdzie nie zmieniają.

pigor: ... Wyznacz zbiór wartości funkcji f(x)= |x−1| + |x+4| ; lub z określenia odległości na osi Ox , dana funkcja f to suma odległości punktów o współrzędnej x od punktów −4 i 1 taka, że dla x∊<−4;1> jest stała równa 5, a na lewo lub prawo od tych punktów −4 lub 1 odpowiednio , czyli dla x∊(−∞;−4) lub x∊(1;+∞) f rośnie do +∞ , a więc f(x)∊<5;+∞) . ...