Oblicz Damian: Mamy trójkąt prostokątny równoramienny i wiem że przeciwprostokątna to 4√2.Jak obliczyć środkową z wierzchołka kąta ostrego? Pilne do poprawki

Piotr: z twierdzenia Pitagorasa

Damian: I jeszcze jedno zadanie : wiem że promień okręgu wpisanego w równoboczny trójkąt jest rowny √3 a jak obliczyć długość boku tego trojkąta? Ps. kumpel polecił mi tą strone i mam nadzieje że ktos wie jak to zadanie powinno wyglądać chodzi potrzebuje wiedzieć jak to sie rozwiązuje z wynikiem bo na tej podstawie będe robił inne zadania. Prosze o pomoc

Damian: A tak jasniej mogłbys mi pokazać jak to sie rozwiązuje?

Damian: ?

konrad:

	1		1		a√3		a√3
r=		h=		*		=
	3		3		2		6

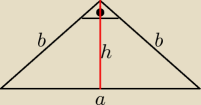
konrad: ad 1. b=4√2 z Pitagorasa liczysz najpierw 'a' a potem też z Pitagorasa liczysz 'h'

Damian: czyli jaki jest koncowy wynik?

konrad: to sobie policz

Damian: a jak mam policzyć z pitagorasa najpier a jak będe miał dwie niewiadome? Mogłbys mi to tak jasno napisac jak to sie liczy? byłbym wdzięczny gdyz potrzebuję na tej podstawie robic inne przykłady a nie jestem pewien czy dobrze to wylicze

ICSP: "Mamy trójkąt prostokątny równoramienny i wiem że przeciwprostokątna to 4√2.Jak obliczyć środkową z wierzchołka kąta ostrego? Pilne do poprawki" Tego się nie liczy Od razu się pisze odp

konrad: a sorry,to przeciwprostokątna jest 4√2...

konrad: czyli do tego rysunku: a=4√3

konrad: znaczy 4√2

pigor: przeciwprostokątna ma dł. 4√2 i Δ prostokątny równoramienny, więc długości przyprostokątnych to a=4 , np z wzoru na dł. przekątnej kwadratu o boku a : a√2, zatem jak poprowadzisz z kąta ostrego środkową s , to tworzy ona trójkąt prostokątny o bokach 4 i ¹₂*4=2 , więc z tw. Pitagorasa masz : s²=2²+4² ⇔ s²=20 ⇒ s=√20 ⇔ s=2√5 − szukana dł.środkowej . ...

ICSP: pigor coś ty zrobił Przecież mamy prostokątny o katach 45, 45. Zatem długość środkowej spuszczonej z wierzchołka kata prostego jest równa promieniowi okręgu opisanego na tym trójkącie czyli połowie przeciwprostokątnej

pigor: ale tam pisze z kąta ostrego ta środkowa

ICSP: To już drugi raz dzisiaj

ICSP: Dobra nic nie pisałem Po prostu nie umiesz czytać

konrad: uu, faktycznie

Damian: A takie pytanko jeszcze z kąd wiemy że a =4? zawsze jest tak? np jak bd miał 5√2 to a = 5?

pigor: ... ja też najpierw tak przeczytałem , ale przecież wtedy to nie byłoby co tam robić .

pigor: tak zawsze , ta liczba a przy pierwiastku , czyli a√2 , to właśnie długość boku kwadratu (tu − u ciebie − połowy kwadratu) . ...

Damian: czyli co?

Damian: ok rozumiem