ciągi Olicha : trzy liczby których suma równa jest 15 tworzą ciąg arytmetyczny. jeśli do pierwszej liczby dodamy 1, do drugiej 4, do trzeciej 19 otrzymamy ciąg geometryczny. znajdź te liczby. w ciągu geometrycznym (a_n), a₃=8, a₆=64, oblicz wyraz pierwszy oraz iloraz ciągu sprawdz czy dany ciąg jest geometryczny: b_n=3²ⁿ⁻² zbadaj monotoniczność ciągu b_n=2n² −1 rozwiąż równanie: 1+4+7+...+(1+3n)=176 wyznacz ciąg geometryczny gdy a₈−a₄=90, a₇−a₅=36 oblicz długość boków i pole trójkąta prostokątnego którego obwód jest równy 120 cm² , wiedząc że długości boków tworzą ciąg arytmetyczny wyznacz ciąg arytmetyczny wiedząc że s₅= 35, s₇=70

Piotr: wszystkie Ci obliczyc ?

ICSP: tak Wreszcie trochę zadanek dla mnie

ICSP: Zad1 trzy liczby : a,b,c których suma jest równa 15 : a+b+c = 15 tworzą ciąg arytmetyczny : 2b = a + c a + b + c = 15 2b = a + c podstawiając : 2b + b = 15 b = 5 a + c = 10 jeśli do pierwszej liczby dodamy 1 : a+1 do drugiej 4 : b+ 4 do trzeciej 19 : c + 19 to otrzymamy ciąg geometryczny : (b+4)² = (a+1)(c+19) mamy wiec układ równań : a+c = 10 ⇒ c = 10 − a 81 = (a+1)(c+19) 81 = (a+1)(10 − a + 19) 81 = (a+1)(−a + 29) 81 = −a² + 28a + 29 a² − 28a + 52 = 0 a² − 2a − 26a + 52 = 0 (a−2)(a−26) = 0 a = 2 v a = 26 mam więc : a = 2 , b = 5 , c = 8 lub a = 26 , b = 5 , c = −16

ICSP: Zad2 a₃ = 8 a₆ = 64 a₁ = ? q = ? a₆ = a₃ * q³ 64 = 8q³ q³ = 8 q³ − 8 = 0 (q−2)(q² + 2q + 4) = 0 ⇒ q = 2 a₃ = a₁ * q² 8 = a₁ * 2² a₁ = 2 odp a₁ = q = 2

ICSP: Zad3 b_n = 3²ⁿ⁻² = 9ⁿ⁻¹ = 1 * 9ⁿ⁻¹ . tak jest geometryczny : a₁ = 1, q = 9

ICSP: Zad4 b_n = 2n² + 1 b_n+1 = 2(n+1)² + 1 = 2(n² + 2n + 1) + 1 = 2n² + 4n + 3 b{n+1 − b_n = 2n² + 4n + 3 − 2n² − 1 = 4n + 2 ∧ 4n + 2 > 0 wiec ciąg jest monotoniczny( stale rosnący) n∊N

ICSP: Zad5 1 + 4 + 7 + ... (3n+1) = 176. ze wzoru na sumę ciagu arytmetycznego :

1 + 3n + 1
	* (n+1) = 176
2

(3n+2)(n+1) − 352 = 0 3n² + 5n − 350 = 0 3n² −30n + 35n − 350 = 0 3n(n−10) + 35(n−10) = 0 (3n+35)(n−10) = 0

	35
n = 10 v n = −		− sprzeczne.
	5

mamy wiec ze n = 10

Piotr: zadanie z trojkatem to obwod raczej to 120 cm bez kwadratu. to sposobem Ety : trojkat prostokatny: 3,4,5 czyli 3a+4a+5a=120 ⇒ a=10 boki trojkata to 30,40,50 P=600

ICSP: Zad6 a₈ − a₄ = 90 a₇ −a₅ = 36 a₄ * q⁴ − a₄ = 90 a₄(q⁴−1) = 90 a₇ − a₅ = 36 a₄q³ − a₄*q = 36

	36
a4q(q2−1) = 36 ⇒ a4 =
	q(q2−1)

36
	* (q4−1) = 90
q(q2−1)

2
	*(q2+1) = 5
q

2q² − 5q + 2 = 0 2q² − 4q − q + 2 = 0 2q(q−2) − 1(q−2) = 0 (q−2)(2q−1) = 0

	1
q = 2 v q =
	2

przypadek pierwszy : q = 2 a₇ − a₅ = 36 a₁*q⁶ −a₁ * q⁴ = 36 64a₁ −16a₁ = 36 48a₁ = 36

	36		3
a1 =		=
	48		4

	3
więc : an =		* 2n−1
	4

	1
przypadek drugi : q =
	2

1		1
	a1 −		a1 = 36
64		16

a₁ − 4a₁ = 2304 −3a₁ = 2304

	2304
a1 =
	−3

	2304		1
an =		* (		)n−1
	−3		2

Piotr: chyba cos sie nie zgadza

ICSP: Zad8 S₅ = 35 S₇ = 70

a1 + a5
	*5 = 35
2

a1 + a7
	*7 = 70
2

a₁ + a₅ = 14 a₁ + a₇ = 20 2a₁ + 4r = 14 2a₁ + 4r + 2r = 20 czyli 2r = 6 ⇒ r = 3 2a₁ + 12 = 14 2a₁ = 2 a₁ = 1 a_n = 3n − 2

Eta: obwód: a−r+a+a+r= 120 ⇒ a= 40

ICSP: prostokąt ≠ trójkąt

ICSP: Zad7 (poprawione) boki : a−r oraz a przeciwprostokątna : a+r 120 = a − r + a + a + r ⇒ 3a = 120 ⇒ a = 40 z twierdzenia Pitagorasa : (a−r)² + a² = (a+r)² a² − 2ar + r² +a² = a² + 2ar + r² a² − 4ar = 0 a(a−4r) = 0 a = 0 − sprzeczne a = 4r ok 40 = 4r ⇒ r = 10 boki : 30,40 przeciwprostokątna : 50

	30 * 40
P =		= 600
	2

Piotr:

Eta: Można było prościej: (a−r)²+a²= (a+r)² ⇒ (a+r)²−(a−r)²= a²

	a
2a*2r= a2 ⇒ r=
	4

Olicha : nie spodziewałam się że to tak łatwe, wystarczy ze spojrzę na początek Waszego zadania jako na podpowiedź i od razu całe zadanie lecę! przydalibyście mi się na egzaminie jako koło ratunkowe DZIĘKUJĘ ŚLICZNIE WSZYSTKIM

Olicha : skąd w zadaniu 5 to czerwone: ^{1 + 3n + 1}₂ * (n+1) = 176 we wzorze przecież jest samo n...

ICSP: Ja bym to nazwał pułapką mamy sume : 1 + 4 + 7 + ... + 3n + 1 i pytamy ile ta suma będzie miała w zależności od n wyrazów. jeżeli podstawimy pod n jedynkę to : 3n + 1 = 4. Czyli suma będzie wyglądała : 1 + 4 czyli dwa wyrazy jeżeli podstawimy dwójkę : 3*2 + 1 = 7 1 + 4 + 7 − trzy wyrazy : dla n = 1 mamy dwa (1 + 1)wyrazy dla n = 2 mamy trzy (2 + 1)wyrazy dla n = 3 mamy cztery (3 + 1_wyrazy ... dla n = n mamy n+1 wyrazów

Basia: można też tak to wyjaśnić a₁ = 1 a₂ = 4 r = 3 stąd a_n = 1+(n−1)*3 = 3n − 2 czyli 3n+1 = 3n−2+3 = 3(n+1)−2 jest n+1 − szym (a nie n−tym) wyrazem ciągu

Gustlik: zad 1. trzy liczby których suma równa jest 15 tworzą ciąg arytmetyczny. jeśli do pierwszej liczby dodamy 1, do drugiej 4, do trzeciej 19 otrzymamy ciąg geometryczny. znajdź te liczby. To mozna zrobić bez układu równań:

	a1+a3		a1+a3
S3=		*3=a2*3, bo		=a2 (mozna tak liczyć, jeżeli średnia arytmetyczna
	2		2

numerow wyrazów jest całkowita) Stąd: a₂*3=15 /:3 a₂=5 Ciąg arytmetyczny: 5−r, 5, 5+r Ciąg geometryczny: 6−r, 9, 24+r Z własności ciągu geom: b²=ac 9²=(6−r)(24+r) 81=144+6r−24r−r² 0=63−18r−r² r²+18r−63=0 Δ=576, √Δ=24, r₁=−21, r₂=3 Sprawdzenie: Dla r₁=−21 mamy: Ciąg arytmetyczny 26, 5, −16, geometryczny 27, 9, 3 Dla r₂=3 mamy: Ciąg arytmetyczny 2, 5, 8, geometryczny 3, 9, 27 Odp: szukane liczby to 26, 5, −16 lub 2, 5, 8.

Gustlik: wyznacz ciąg arytmetyczny wiedząc że s5= 35, s7=70

	a1+a5
S5=		*5=a3*5 (metoda średniej arytmetycznej opisana w poście powyżej)
	2

	a1+a7
S7=		*7=a4*7
	2

a₃*5=35 /:5 a₃=7 a₄*7=70 /:7 a₄=10 a₄−a₃=r 10−7=r r=3 a₁=a₃−2r=7−2*3=1 a_n=a₁+(n−1)*r=1+(n−1)*3=1+3n−3=3n−2 Odp: a_n=3n−2

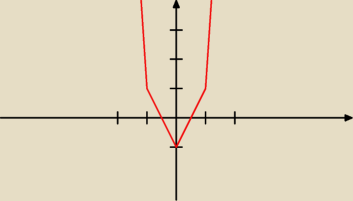
Gustlik: zbadaj monotoniczność ciągu bn=2n² −1 Można funkcją − rysuję wykres funkcji y=2x²−1 (trochę połamana ta parabola, ale źle są wyświetlane krzywe, nie wiem czemu), wiemy że dziedzina ciagu to N₊, a dla dodatnich liczb ta funkcja rośnie − można to odczytać z wykresu, zatem ciąg a_n jest rosnący.

Olicha : JESTEŚCIE BOSYCY! gdyby nie Wy w życiu nie nauczyłabym się do poprawki z matematyki.. co prawda dopiero we wtorek okaże się czy zdam, ale teraz czuję się o wiele mocniejsza i przygotowana, a każdemu z Was należy się ode mnie stokrotne dzięki

Gustlik: Olicha, zdasz na pewno ! Pozdrawiam

Olicha : NO TO ZDAŁAM! na 3! i wszystko zawdzięczam Wam! Wielkie dzięki!

Gustlik: SUPER ! Pozdrawiam