geometria analityczna Ania: 4.wie ktos może jak zrobić to zadanie?: Bok AB trójkąta ABC zawiera się w prostej y=2x+2, a środkowa poprowadzona z wierzchołka C zawiera się w prostej x – 3y +21 = 0. Wiedząc , że wektor BC =[4, −2] oblicz współrzędne wierzchołków trójkąta ABC.

@Basia: Pomagam

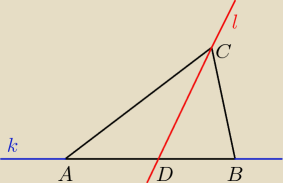
@Basia: punkt D jest punktem wspólnym prostych k: y=2x+2 l: x−3y+31=0 wyznacz jego współrzędne (czyli rozwiąż układ równań) D jest środkiem odcinka AB

	xa+xb
xd =
	2

	ya+yb
yd =
	2

ponadto A,B,D∊k y_d = 2x_d+2 y_a=2x_a+2 y_b=2x_b+2 stąd będzie jedno równanie dla x_a,x_b i jedno dla y_a,y_b albo prościej AD^→=DB^→ z zapisu współrzędnych BC^→ dostaniesz równania z x_b,x_c i y b,y_c podstawiając za x_c 3y_c−21 i za y_b 2x_b+2 dostaniesz układ dwóch równań z niewiadomymi y_c i x_b wylicz je dalej już łatwo

Ania: dziękuje