zadanie, geometria filip: Kąt zewnętrzny przy podstawie trójkąta równoramiennego jest większy o 36st. od kąta zewnętrznego przy jego wierzchołku. Wyznacz kąty tego trójkąta.

@Basia: Pomagam

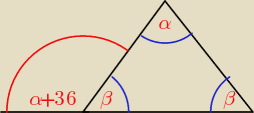
@Basia: zastanów się ile to jest: α+36+β = ? α+β+β = ? a następnie rozwiąż układ równań

filip: nie wychodzi mi:( a czy α na pewno jest dobrze w tym ukłądzie równan, jako kąt zewnętrzny?

@Basia: oj przepraszam; nie doczytałam, że przy wierzchołku też zewnętrzny; zaraz poprawimy

Klara: Kąt zewnętrzny trójkąta = sumie katów wewnętrznych do niego nie przyległych więc kat zewnetrzny przy podstawie = α+β a kat zewnętrzny przy wierzchołku to : β+β wiec masz równanie: α+β= 2β+36^o i suma katów wewnętrznych jest: α+ 2β= 180^o rozwiąz teraz układ tych dwu równań i oblicz α i β

Klara: otrzymasz: α − β= 36^o α+2β= 180^o już sobie poradzisz

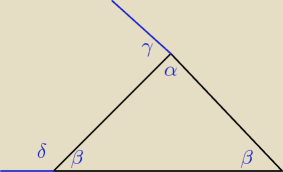
@Basia: α+γ=180 γ=180−α δ=γ+36=180−α+36 δ+β=180 180−α+36+β=180 −α+β=−36 /*(−1) α−β=36 /*2 α+2β=180 2α−2β=72 α +2β=180 −−−−−−−−−−−−−−−−−−−− 3α=252 α=84 84−β=36 −β=−48 β=48

filip: dziekuje wszystkim za pomoc