Układ nierówności. Mila: Zadanie dla asdf i Saizou Rozwiąż algebraicznie i graficznie układ nierówności: | |x| −|y||≤2 |x+y|+|x−y|≤ 6 Eta , ICSP, Godzio, Basia nie pomagają. Do skutku.Pomoże im wolfram i to wystarczy.

Saizou : Mila ja jeszcze mam zadanie od Ciebie i od Godzia, a może jeszcze zrobię zadania od Gustlika

Artur z miasta Neptuna: A ja mogę pomagać ... jak dobrze ... a więc:

Mila: Arturku, nie możesz. Czekamy, aż nasze młode orły to zrobią, poradzą sobie.

Artur z miasta Neptuna: ale ale ... ja też chcę się znowu poczuć jak młody orzeł

Mila: dla Artura.

Eta:

Saizou : w pierwszym będzie kwadrat o wierzchołkach (0:2) (0:−2) (2:0) (−2:0)

Artur z miasta Neptuna: nein

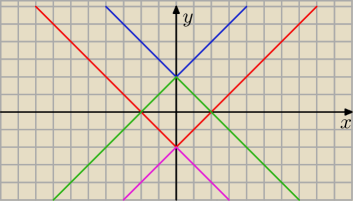
Saizou : llxl−lyll≤2 lxl−lyl≤2 i lxl−lyl≥−2 wystarczy sprawdzić tę nierówność I dla y≥0 lxl−2≤y oraz lxl+2≥y II dla y<0 y≤−lxl+2 oraz y≥−lxl−2 zaznaczając nierówności na układzie współrzędnych otrzymujemy taki jakby iks

Ajtek: Jakbym ze trzy dni pomyślał, to być może, z naciskeim na być może, rozwiązałbym to zadanko... Dobry wieczór Eta, Mila, Artur..., Saizou .

Saizou : witaj Ajtek wcale to nie było takie trudne

Ajtek: Hej, hej Saizou. Ja mam wielkiego, wakacyjnego, matematycznego lenia Miałem sobie przypomnieć przez te wakacje wiele zagadnień z matmy. Chciałem zacząć od macierzy, a na całkach skończyć. Macierze zacząłem i na nich skończyłem .

Saizou : lepiej mieć lenia niż dobre chcęci bo " dobrymi chęciami droga do piekła jest wybrukowana"

Ajtek: No właśnie miałem dobre chęci, tylko motywacji zabrakło.

Saizou : Ajtek mogę Cię pocieszyć że ja też nie mam motywacji na stan obecny

Ajtek: Saizou, ale Ty cokolwiek robisz. Natomiast ja, poza wyciągnięciem zeszytu akademickiego i ksiązki ze studiów, faktycznie nie zrobiłem nic!

Saizou : ale książki wyciągnąłeś

Mila: Witam, Ajtek, to miło, że jesteś. Saizou, pięknie, ale to dopiero I nierówność i punkty w tym "krzyżyku". Dalej, rysować potrafisz. Podpowiedź: A) x+y≥0 i ....dwa warunki B) x+y<0 i ...

Ajtek: No wyciągnąłem i kurz zbierają. A nie o to mi chodziło. Czekam jeszcze na "Poradnik matematyczny", brat ma mi przywieźć w weekend, może to mnie do pracy zmobilizuje.

Ajtek: Hej, hej Mila. Jestem, a jednak mnie nie ma

Saizou : tak Mila chodzi o przestrzeń między kolorowymi liniami włączając linie

Saizou : Mila przeczysz sama sobie bo miało być bez podpowiedzi

Godzio: Ale mnie kusi taka ładna podpowiedź, ale jak nie mogę to nie mogę

Mila: Wynik, rzeczywiście ładny.Zostawmy to dla Saizou. Dobranoc.

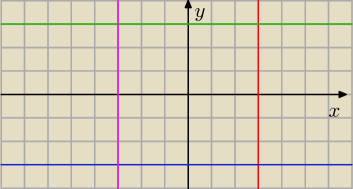
Saizou : lx+yl+lx−yl≤6 I dla x≥−y i x≥y x+y+x−y≤6 x≤3 II dla x≥−y i x<y −x−y+x−y≤3 y≥−3 III dla x<−y i x≥y x+y−x+y≤6 y≤3 IV dla x<−y i x<y −x−y−x+y≤6 x≥−3 zatem otrzymujemy kwadrat

asdf: @Mila Dzięki za zadanie, ale pierw to ja ogarnę wartość bezwzględną nie robiłem jej zbyt często

Saizou : Mila dobrze to jest rozwiązane

Mila: Teraz należy połączyć warunki ( I i II równanie) .

Mila: Wynik, dobry, zaraz sprawdzę po kolei Twoje obliczenia.

Mila: Popraw obliczenia w II i III warunku, zrobiłeś tzw. czeski błąd.

Saizou : II −x−y+x−y≤6 −2y≤6 y≥−3 III x+y−x+y≤6 2y≤6 y≤3

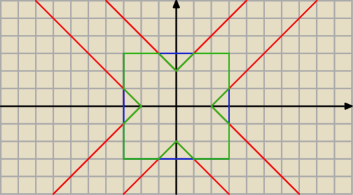
Saizou : ostatecznie zostaje kolor zielony znaczy się przestrzeń ograniczona kolorem zielonym z liniami

Mila: Obszar bardzo dobrze. II) x+y≥0 (y≥−x obszar nad prostą ) i x−y≥0 x+y+x−y≤6 2x≤6 x≤3 III) x+y<0 i x−y≥0 −x−y+x−y≤6 −2y≤6 y≥−3

Krzychu: Ja mam pytanie donośnie tego zadania. Jak mam warunek do drugiej nierówności x≤−y to jak opuscić wartość bezwzględną z |x−y| ?

.: idzie garbaty o polnocy przez cmentarz i spotyka diabla ten sie go pyta: −masz pieniadze −nie −a co masz −garb − to dawaj nastepnego dnia idzie uradowany juz wyprostowany garbaty i spotyka kulawego. Opowiedzial mu cala historie i kulawy prubuje swoich sil. wyskakuje diabel i sie pyta: −ej masz pieniadze −nie −a masz garba −nie −to masz

Krzychu: Wróćmy może jednak do pytania

Mila: Rozważam warunki: x−y≥0 ⇔|x−y|=^dfx−y x−y<0⇔|x−y|=^df−x+y

Krzychu: ^df pierwszy raz to widzę

Krzychu: ale już sobie poradziłem, wyszło mi tak samo.

Mila: To oznacza z definicji .