s szklanka: Pokaż że jeżeli a,b,c, należy do przedziału < 0;1 >,to

	1
abc (1−a) (1−b) (1−c) <=
	64

Mam tylko pytanie Przedostatnia wiadomość↓ http://forum.zadania.info/viewtopic.php?f=25&t=5110 Rozumiem to rozwiązanie ,ale o co chodzi z tym przedziałem W ogóle go tam nie uwzględniamy czy jak?

Mila: Jeśli a, b, c należą do tego przedziału to 1−a≥0 itd

szklanka: Sory teraz jest dobrze↓ Pokaż że jeżeli a,b,c, należy do przedziału < 0;1 >,to ↓

	1
abc(1−a)(1−b)(1−b) ≤
	64

Jeśli a, b, c należą do tego przedziału to 1−a≥0 ←dlaczego większe bądź równe ?

asdf: @Mila Witam, 1) Jaka jest różnica między takim zapisem: 1 − a ≥ 0 a takim zapisem: a ∊ <0; 1> 2) Można jakąś podpowiedź jeszcze do zadania?

szklanka: nie wiem teraz o co Ci chodzi ASDF, chcę tylko aby ktoś odpowiedział na MOJE OSTATNIE PYTANIE TUTAJ

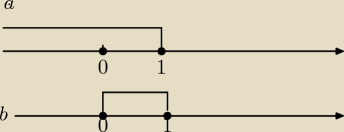
Mila: 1) szklanka a∊<0,1>⇔ 0≤a≤1 ⇔a≥0 i a≤1 a≤1 /−a 0≤1−a ⇔1−a≥0 2) asdf ilustracja graficzna a) x≤1 b) x∊<0;1>

asdf: @Mila Chyba się nie zrozumieliśmy, jaka jest różnica między zapisem: 1 − a ≥ 0 a takim zapisem: a ∊ <0;1> Nie zrozumiałem Twojej podpowiedzi(?) z 19:15 dlatego pytam

szklanka: Czyli w tym zadaniu przy rozwiązywaniu tego zadania nie trzeba się przejmować jakimś przedziałem ponieważ on dotyczy i jest zawarty w treści, tak?

asdf: @Mila nie było pytania...

Bogdan: Trzeba przejmować się podanym założeniem. Tutaj a∊<0, 1> i b∊<0, 1> i c∊<0, 1> czyli żadna z tych liczb nie jest ujemna i nie jest większa od 1, a mówiąc jeszcze inaczej, a, b, c to ułamki właściwe lub mogą przyjmować wartość zero lub 1.

Mila: Inny dowód . f(a)=a−a² i a∊<0,1>

	1
aw =		∊<0,1>
	2

	1
f(1/2)=		− największa wartość f(a)
	4

	1
Zbiór wartości <0,		>
	4

Analogicznie dla g(b)=b−b² h(c)=c−c²

	1
a−a2≤
	4

	1
b−b2≤
	4

	1
c−c2≤
	4

stąd

	1
(a−a2)(b−b2)(c−c2)≤
	64

szklanka: Mila podoba mi sie Twój sposób ,ale powiedz mi jak doszłaś do drugiej linijki

Artur_z_miasta_Neptuna: które ile wynosi a_w zapraszam do wzorów: https://matematykaszkolna.pl/strona/79.html

szklanka: i jeszcze to f(a)=a−a² ←to jakiś wzór? A a_w ← co to oznaczało?

Vax:

	a+b+c+(1−a)+(1−b)+(1−c)		1
Z am−gm mamy 6√abc(1−a)(1−b)(1−c) ≤		=		⇔
	6		2

	1
abc(1−a)(1−b)(1−c) ≤
	64

szklanka: Vax, nie wiem o co Ci idze, to co przedstawiłeś do czego się odnosi?

ICSP: Najprostsze udowodnienie

Vax: Do tezy zadania

szklanka: może i jest , ale i tak tego Twojego sposobu nie rozumiem

b.:

	x + (1−x)		1
√x(1−x) ≤		=		dla x∊[0,1]
	2		2

stąd

	1
x(1−x) ≤
	4

stosując do x=a, x=b, x=c i wymnażając stronami dostaje się tezę