calki podwojne anka: witam, mam problem z tym zadaniem: mam obliczyć objętość bryły ograniczonej powierzchnią: x²+y²+2x=0, a mam to obliczyć za pomocą postaci biegunowej

bumblebee: kurcze zebym ja wiedzial co to jest postac biegunowa

♊: bumblebee: całki to na studiach dopiero są ;) anka: niestety z moją wiedzą z zakresu całek mogę tylko przyposzczać, że mamy do czynienia z kulą bądź sfrerą. @Basia: to wyżej to znak dla Ciebie, że nie zrobię tego zadania i zostawiam Tobie (bądź też innym zainteresowanym) to proste _{(jeżeli posiada się odpowiednią wiedzę)} zadanie ;)

anka: no właśnie ono nie jest takie proste.... a postacią biegunową wyliczyć je łatwiej... podobno

@Basia: Równanie, które podałaś nie jest równaniem powierzchni tylko równaniem zwykłego płaskiego okręgu. O jaką więc powierzchnię chodzi ? Jeżeli z jest dowolne to powierzchnia takiego "nieskończonego" walca też będzie nieskończona. Czyli coś tu nie gra.

anka: bo ja nie wiem jak to ugryść, a nie jestem taka beznadziejna z matmy faktycznie coś tu nie halo w poleceniu, bo to wyjdzie płaska figura... ale tak mi podał Pan Doktor...

Michał Szczotka: a to chyba jakiś stomatolog ci to podał

anka: też się czasami zastanawiam za co on doktorat dostał....

@Basia: Jestem pewna, że trzeba obliczyć całkę podwójną po podanym kole. Ale z czego ? To musi być podane w zadaniu. A jeśli nie to musisz zgłosić panu doktorowi uzasadnione pretensje. Oczywiście, że całkować po kole jest łatwiej korzystając ze współrzędnych biegunowych, ale trzeba mieć to coś do całkowania.

@Basia: Tak to mniej więcej musi wyglądać: Obliczyc całke podwójna

	dxdy
∬		, gdzie D jest kołem x2 + y2 ≤ 4.
	√x2+y2

D

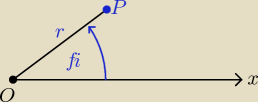
Bogdan: Jest okazja, by przybliżyć układ współrzędnych biegunowych na płaszczyźnie. Podaję się w tym układzie punkt O zwany biegunem oraz półprostą Ox wychodzącą z punktu O zwaną osią biegunową, określa się jednostki długości oraz kierunek odkładania kąta. Współrzędnymi biegunowymi punktu P różnego od bieguna O nazywamy: − odległość r punktu P od bieguna O zwaną promieniem wodzącym, − kąt φ między osią biegunową Ox i promieniem OP zwany argumentem. Główną wartością argumentu punktu P nazywamy kąt φ ∊ <0, 2π>. Jeśli φ_o jest jedną z wartości argumentu jakiegoś punktu, to każda inna wartość argumentu φ tego punktu spełnia warunek φ = φ_o + k*2π, gdzie k ∊ C. Punkt P zapisujemy: P = (r, φ). Jeśli biegun O pokrywa się z początkiem prostokątnego układu współrzędnych Oxy, a oś biegunowa jest dodatnią częścią osi x, P = (r, φ) oraz P = (x, y), to:

	x		y
r = √x2 + y2, cosφ =		, sinφ =		,
	r		r

oraz x = rcosφ, y = rsinφ Przykład: W prostokątnym układzie współrzędnych okrąg podany w zadaniu wyraża się wzorem x² + y² + 2x = 0 lub (x + 1)² + y² = 1, środek okręgu S = (−1, 0), R = 1. Ten sam okrąg w biegunowym układzie współrzędnych ma postać: (rcosφ + 1)² + r²sinφ = 1 ⇒ r²cos²φ + 2rcosφ + 1 + r²sin²φ = 1 ⇒ ⇒ r²(cos²φ + sin²φ) + 2rcosφ = 0 ⇒ r + 2cosφ = 0. Ostatecznie otrzymujemy wzór: r = −2cosφ