Wykaż, że w trójkącie ABC... Kamila: Wykaż, że w trójkącie ABC kąt między wysokością opuszczoną z wierzchołka A i dwusieczną kąta A równa się połowie różnicy kąów B i C.

miśka: moze podobienstwo trojkatow?

Kamila: Ale jak mam je zastosować do tego zadania...?

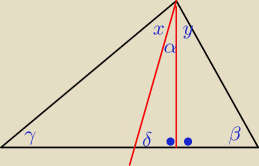
@Basia: α+y = x x+γ+z = 180 za x wstawiam α+y α+y+γ+z = 180 α+y+δ+β=180 −−−−−−−−−−−−−−−−−−−−− 2α+2y+y+z+δ+β=360 2α = 360−2y−γ−z−δ−β z=180−δ y=90−β 2α=360−2(90−β)−γ−(180−δ)−δ−β 2α=360−180+2β−γ−180+δ−δ−β 2α=β−γ α=^β−γ₂

@Basia: Miśka tu nie ma żadnych trójkątów podobnych

Kamila: Dzięki Postaram się rozkminić

Klara: Można też tak: α+x +γ= 90^o −−−− to w trójkącie prostokątnym po lewej stronie β+y = 90^o −−−− " " " " prawej dodatkowo x = y +α −−− bo to kąty równe ( dwusieczna) więc: α+y +α+γ= β+y 2α= β − γ to α= ^{β − γ}₂

Kamila: Dzięki wam obu Już chyba mniej więcej rozumiem.

Klara: Miło nam

13LateK: a gdzie tutaj na rysunku jest Z?

BlackMoorgan665: Gdzie jest z?

Krzysiek : A co napisala Basia. z=180−δ . teraz popatrz na pierwszy trojkat z lewej i masz kat γ i kat x wiec gdzie bedzie kat z