Wybaczcie że tutaj Neko: Ale nie wiem gdzie napisać : ) Może pan Jakub dodać to ? http://www.cke.home.pl/dokumenty/sierpien2012/matematyka/matematyka_PP.pdf Sierpień 2012.

Eta: Poczekaj, cierpliwie, Jakub z pewnością umieści ten arkusz w temacie matur!

tomek: Nie wie ktoś czasem czy była/będzie matura poprawkowa ale rozszerzona z matematyki?

Saizou : zad 1. k₂ jest o 10% większe do k₁, zatem k₂=1,1k₁ zatem P_k2=(1,1k₁)²=1,21k₁² P_k1=k₁²

1,21k12−k12
	*100%=0,21*100%=21%
k12

Saizou : zad 2 9⁻⁵*3⁸=(3²)⁻⁵*3⁸=3⁻¹⁰*3⁸=3⁻²=9⁻¹

Saizou : zad 3 log₃27=x 3^x=27 3^x=3³ x=3 log₃1 korzystając ze wzoru log_a1=0 log₃1=0 zatem log₃27−log₃1=3−0=3

Saizou : zad 4 (2−3√2)²=4−2*2*3√3+9*2=4−12√2+18=22−12√2

Saizou : zad 5 f(x)=mx+2 f(−2)=0 0=−2m+2 2m=2 m=1

Saizou : zad 6 lx+4l≤7 x+4≤7 ⋀ x+4≥−7 x≤3 ⋀ x≥−11 x∊<−11:3>

Saizou : zad 7 y=x²+8x−14

	−b		−8
Wx=		=		=−4
	2a		2

Saizou : zad 8 zbiór wartości czyli zbiór igreków, zatem odpowiedź B

Tina: haha zdałam zdałam zdałam

Saizou : zad 9 x(x+6)<0 x=0 lub x+6=0 x=−6 x∊(−6:0)

Eta:

Saizou : zad 10 x⁶+x³−2=0 zróbmy podstawienie x³=t t²+t−2=0 Δ=1+8=9 √Δ=3

	−1−3
t1=		=−2
	2

	−1+3
t2=		=1
	2

(t+2)(t−1)=0 (x³+2)(x³−1)=0

Eta: x⁶ −x³+2x³ −2=x³(x³−1) +2(x³−1)=(x³−1)(x³+2)

Saizou : zad 11

(x+3)(x−2)
	=0
(x−3)(x+2)

zał: (x−3)(x+2)≠0⇔x≠3 lub x≠−2

	(x+3)(x−2)
ale żeby		=0 to licznik musi być równy zero zatem
	(x−3)(x+2)

x+3=0 lub x−2=0 x=−3 lub x=2 zatem ma dwa rozwiązania

Saizou : zad 12

	n
an=		dla n≥1
	(−2)n

	3		3		3
a3=		=		=−
	(−2)3		−8		8

Saizou : zad 13 a_n=a₁*qⁿ⁻¹ 18=36*q²⁻¹ 18=36*q¹ 18=36q

	1
q=
	2

	1		1		1
a4=36*(		)4−1=36*(		)3=36*		=4,5
	2		2		8

Saizou : zad 14

	7
sinα=
	13

z tw. Pitagorasa mamy że 7²+a²=13² a²=120 a=√120

	7		7
zatem tgα=		=
	a		√120

Eta:

	a2
q=
	a1

	a2
a4= a2*(		)2
	a1

	a23		18*18*18
a4=		=		= 4,5
	a12		36*36

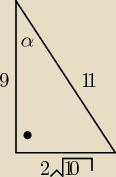
Saizou : zad 15

	2√10
sinα=
	11

	9
cosα=
	11

	2√10
tgα=
	9

	9
ctgα=
	2√10

Bogdan: zad. 13

	18		1		1		1
q =		=		, a4 = 18 * q * q = 18 *		*		= 4,5
	36		2		2		2

Eta:

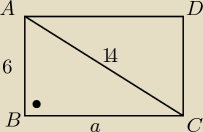
Saizou : zad 16 a²+6²=14² a²=160 a=√160=4√10

Saizou : zad 17 z tw o kącie wpisanym i środkowym mamy że

	1
∡ACB=		*230=115
	2

Eta: Ale się zawziąłeś

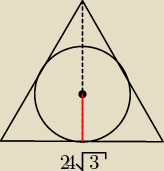
Saizou : zad 18

	1
r=		h
	3

	a√3
h=
	2

	24√3*√3
h=		=36
	2

	1
r=		*36=12
	3

Saizou : Eto ciekaw jestem czy zdam zad 19

	1
y=−		x+2
	3

z prostopadłości prostych mamy że a₁*a₂=−1

	1
−		*a2=−1
	3

−a₂=−3 a₂=3 P=(0:0) 0=3*0=b b=0 ostatczenie wzór prostej to l: y=3x

Bogdan: zad. 18

	1
Nie potrzeba tutaj wyznaczać h (to jakaś powszechna maniera), przecież r =		a√3
	6

	1
W tym zadaniu r =		*24√3*√3 = 12
	6

Eta: Za dużo tych "drobiazgów" ( czasu Ci zabraknie zad 19 prosta jest postaci y= ax ( niepotrzebnie wyznaczasz "b"

Eta:

	a√3
Zad; 18 r=		to r=.....
	6

Bogdan: zad. 19 Prosta przechodząca przez początek układu współrzędnych ma równanie y = ax Tu od razu widać (na podstawie warunku prostopadłości), że a = 3, a więc y = 3x

Eta:

Saizou : zad 20 x²=7²+3² x²=58 P=x²=58

Saizou : wiem że można by zastosować wzór na dł. docinak w układzie współrzędnych

Saizou : zad 21 S=(a:b) r²=(x−a)²+(y−b)² 100=(x+4)²+(y−6)² a=−4 b=6 S=(−4:6)

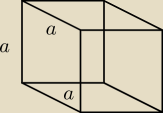
Saizou : zad 22 V=a³ 64=a³ a=4 P_c=6*a²=6*4²=96

Saizou : zad 23

	1
V=		πr2H
	3

	1		a2
r2=(		a)2=
	2		4

	a√3
H=
	2

	1		a2		a√3		√3
V=		*π*		*		=		a2π
	2		4		2		8

Saizou :

	√3
poprawka		a3π
	8

Eta:

Saizou : zad 24 2000 , 2800 , 3400 , 3600 , 4200 ,8000

	3400+3600
mediana=		=3500
	2

Eta: w mianowniku 24

Eta: Oczywiście w zad, 23

Saizou : tak przeliczyłem to jeszcze raz i teraz mi się zgadza

Saizou : zad 25 Ω=={1,2,3,4,5,6,7,8,9,10,11,12,13,14,14}=15 A={4,8,12}=3

	3		1
P(A)=		=
	15		5

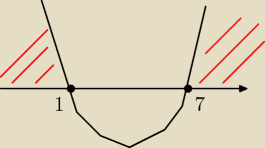
Saizou : zad 26 x²−8x+7≥0 Δ=64−28=36 √Δ=6

	8−6
x1=		=1
	2

	8+6
x2=		=7
	2

x∊(−∞:1>∪<7:+∞)

Saizou : x³−6x²−9x+54=0 x²(x−6)−9(x−6)=0 (x−6)(x²−9)=0 (x−6)(x+3)(x−3)=0 x=6 lub x=−3 lub x=3

Eta: zad26 (bez delty) x²−8x+7 = (x−1)(x−7) ≥0

Saizou : zad 28 a₁=3 a₄=15 15=3+3r 12=3r r=4 a₆=3+5*4=23

	3+23
S6=		*6=78
	2

Saizou : zad 29 AD=h BC=a =6

	ah		6h
P=		=		=3h
	2		2

	1		36		1
P=		*62*sin30=		*		=9
	2		2		2

9=3h h=3

Saizou : zad 30 na razie ominę (ale wrócę) zad 31 Zał :c<0 Teza: trójmian: x²+bx+c ma dwa miejsca zerowe Dowód: Δ=b²−4c iloczyn −4*c jest zawsze dodatni, zatem delta jest dodatnia, wówczas trójmian ma dwa różne miejsca zerowe ckd

Jakub: Łał szybcy jesteście Ja dopiero 6 zadań dodałem 3513.

Saizou : ja jestem już zmęczony ale jutro dokończę więc mówię dobranoc

Neko: Zadanie za 5 punktów vt=114 (v−9,5)(t+2)=114 vt+2v−9,5t−19=vt /−vt 2v=9,5t+19/*2 4v=19t+38/:4 v=¹⁹₄t+9,5 Podstawiamy do do 1 równania i mamy 19t²+38t−456=0 Δ=1444+34656=190² t1={−38+190}{38}=4 t2={−38−190}{38}=−6 t2 odrzucamy bo czas nie może być ujemny 4v=114 v=28,5 Odp 28,5 km/h

Saizou : zad. 32 dł. odcinak AC=√(1−2)²+(1−9)²=√65 teraz narysujmy okrąg w środku C i promieniu AC napiszmy wzór okręgu (x−1)²+(y−9)²=65 tworząc układ równań (x−1)²+(y−9)²=65²

	1
y=		x
	2

Obliczając otrzymujemy x₁=2 y₁=1 oraz

	34		17
x2=		y2=
	5		5

	34		17
Zatem szukany punkt "B" ma współrzędne (		:		)
	5		5

Bogdan: Zadanie 34. (5 pkt) Kolarz pokonał trasę 114 km. Gdyby jechał ze średnią prędkością mniejszą o 9,5 km/h, to pokonałby tę trasę w czasie o 2 godziny dłuższym. Oblicz, z jaką średnią prędkością jechał ten kolarz. Takie zadanie (chodzi o sposób rozwiązania) jest prawie w każdym arkuszu maturalnym. Proponuję następujący zapis rozwiązania tego zadania. Oznaczenia (koniecznie): v − rzeczywista prędkość kolarza, v > 0 t − rzeczywisty czas jazdy kolarza z prędkością v, t > 0 (v − 9,5) − planowana prędkość kolarza, v − 9,5 > 0 (t + 2) − planowany czas jazdy kolarza z prędkością (v − 9,5), t + 2 > 0 ( * ) vt = 114

	19		19
(**) (v −		)(t + 2) = 114 ⇒ 114 + 2v −		t − 19 = 114 ⇒
	2		2

	19		4
⇒		t = 2v − 19 ⇒ t =		v − 2
	2		19

(wyznaczamy t, a nie v, bo pytanie w zadaniu dotyczy v)

	4
( * )		v2 − 2v − 114 = 0 /*19 ⇒ 4v2 − 38v − 2166 = 0,
	19

Δ = 36100, √Δ = 190

	38 − 190		38 + 190
v =		< 0 lub v =		= 28,5
	8		8

(t nie wyznaczamy, bo nie potrzeba) Odp.: v = 28,5 km/godz.

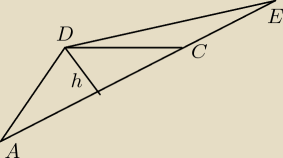
Grześ1992: |AC|=a ; |CE|=a/2 P_ACD=ah ; P_CDE=ah/2 P_rombu=2ah

Prombu
	=4
PCDE

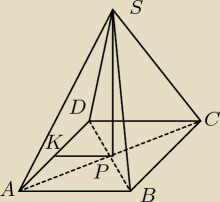
Saizou : zad 33

	8√3
trójkąt ACS jest równoboczny o boku 8 zatem SP=h=		=4√3
	2

AC=8 i jest przekątną kwadratu ABCD zatem bok tego kwadratu wynosi AD=AB=4√2

	1
DK=AK=KP=		AB=2√2
	2

z tw. Pitagorasa mamy że (2√2)²+(4√3)²=lKSl² lKSl²=56 KS=√56=2√14

	SP		4√3		√42
sinα=		=		=
	KS		2√14		7

Grześ1992: P_ACD=ah/2 P_CDE=ah/4 P_rombu=ah P_rombu/P_CDE = 4 sorki zgubilem cos po drodze heh

Saizou : zad 30 zał: rysunek teza: P_ABCD=4P_CDE dowód: P_ABCD=2P_ACD zauważmy że h jest wysokością ΔACD i ΔCDE

	1
PACD=		2x*h=xh
	2

	1
PCED=		h*x={hx}{2}
	2

zatem P_ACD=2P_CED wówczas P_ABCD=2*P_ACD=4P_CDE cnu

Bogdan: Podam ciekawostkę związaną z zadaniem 33 o ostrosłupie. W ostrosłupie prawidłowym n−kątnym: β − miara kąta nachylenia krawędzi bocznej do płaszczyzny podstawy, α − miara kąta nachylenia ściany bocznej do płaszczyzny podstawy, α, β są kątami ostrymi.

	π
zachodzi zależność: cos		* tgα * ctgβ = 1
	n

	180o
albo biorąc miary kątów w stopniach: cos		* tgα * ctgβ = 1
	n

W zadaniu nr 33: β = 60^o, n = 4 (bo jest ostrosłup prawidłowym czworokątnym)

	180o		√2		√3
cos		= cos45o =		, ctg60o =
	4		2		3

Mamy więc równanie:

√2		√3
	*		* tgα = 1 / *√6 ⇒
2		3

	√6		√42
⇒ tgα = √6 ⇒ sinα =		=
	√7		7

akacja: Gdy w zad 34 zapisałam xy=114 bez znaku mnożenia to dostanę 1 punkt czy nie

akacja: x3−6x2−9x+54=0 x2(x−6)−9(x−6)=0 (x−6)(x2−9)=0 Jeśli doszłam do tego momentu a potem zamiast rozbić napisałam x1 6 x2 nie ma to będzie 1 czy 0