Prosta i płaszczyzna w R3 The Sun: Dla czworościanu o wierzchołkach A(0,1,2), B(3,2,1),C(−1,0,2) D(2,3,3) wyznaczyć miarę kąta między wysokością wychodzącą z wierzchołka A w trójkącie ABC a ścianą tego czworościanu zawierającą wierzchołki BCD

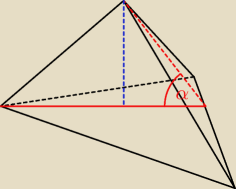
Artur z miasta Neptuna: wskazówka

The Sun: Tyle to ja wiem.Wyznaczyłam wektor kierunkowy wysokości i wektor normalny płaszczyzny.Podstawiłam do wzoru na sinus kata między nimi ,ale nie wychodzi tak jak w odpowiedzi.

Bogdan: Proponuję wyznaczyć równanie płaszczyzny π₁ zawierającej punkty: A, B, C: A₁x + B₁y + C₁z + D₁ = 0 oraz równanie płaszczyzny π₂ zawierającej punkty: B, C, D: A₂x + B₂y + C₂z + D₂ = 0 a następnie kąt α między tymi płaszczyznami wg zależności:

	|A1A2 + B1B2 + C1C2|
cosα =
	√A12 + B12 + C12 * √A22 + B22 + C22

pigor: ...a jaką masz odpowiedź no i podaj te swoje wektory to ...pogadamy . ...