mam poprawke z matmy na uz
barbaksia: mam poprawkę z matmy i nie wiem jak rozwiązać te zadania, czy ktoś może pomóc. Matme miałam
wieki temu. Z góry dziękuję
oto zadanka :
1. oblicz granicę: lim x→0 sinx/ln(1+x)
2.czy funkcja jest róznowartościowa ? wyznacz f. odwrotną f(x)= x /1+x
3.oblicz całkę ∫x(x−1)2 +1 całka o górnej granicy 2 i dolnej 0
4.zbadaj przebieg zmiennosci funkcji f(x)= x(x−1)2 +1
21 sie 10:55
o nie: | | 0 | |
1) granica |
| −> de l'hospital się narzuca aż |
| | 0 | |
| sin(x) | | cos(x)*(x+1) | |
| =H= |
| −>01 |
| ln(1+x) | | 1 | |
21 sie 11:53
o nie: nie umiem zrobić strzałki z zerem pod spodem ale chyba wiadomo że chodzi mi o "granica gdy x
dąży do 0"
3)
masz pod całką x
3 −2x
2+x+1 po rozbiciu nawiasu, liczysz każdą całke oddzielnie i voila:
reszta analogicznie, sumujesz wyniki całek
21 sie 12:07
ania:
2. jest różnowartościowa
3. całka to 1/4x4 −2/3x3+1/2x2+x = 223
21 sie 12:12
o nie: 4) szczerze mówiąc tak samo bym rozbił nawias żeby granice łatwo sie liczyło.
dziedzina R
lim
−∞ x(x+1)
2+1=lim
−∞ x * lim
−∞ (x+1)
2=−
∞ *
∞ = −
∞
analogicznie lim
∞
pierwsza pochodna x
3−2x
2+x+1 = 3x
2−4x+1 określa punkty przegięcia
druga pochodna = 6x−4 określa czy funkcja jest wklęsła czy wypukła
wszystkie dane zbierasz w tabelkę i rysunek
21 sie 12:20
ania:
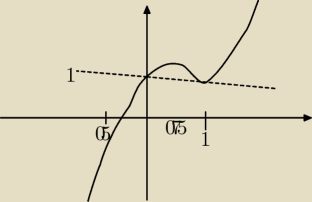
21 sie 12:21
ania: o nie..nie mów że dodałeś x3 z x2
21 sie 12:22
21 sie 12:24
barbaksia: jesteście kochani i tacy szybcy. a jak udowodnić że ta funkcja z zad 2 jest różnowartościowa?
21 sie 12:24
o nie: gdzie?
21 sie 12:25
o nie: właśnie nie wiem czy chodzi o to że jest nieokreślona w zerze i nieskończonościach czy że dąży
do różnych wartości dla tych samych y−ków?
21 sie 12:26
o nie: nie dodałem tylko pierwszy nawias źle zapisałem w granicy w 4tym zadaniu jeśli o to chodzi
21 sie 12:29
ania: źle spojrzałam..to juz pochodna była ;> przepraszam

21 sie 13:04
ania: różnowartościowa to znaczy że dla każdego x ma inną wartość y
21 sie 13:05
ania: funkcja odwrotna to zamieniasz x na y i y na x i wyliczasz y
x+xy=y
x=y−xy
x=y(1−x)
| x | |
| =y to jest funkcja odwrotna
|
| 1−x | |
21 sie 13:08
ania: różnowartościowa bo :
założenie: x
1 ≠ x
2 ==> x
1 − x
2 ≠ 0
więc f(x
1)−f(x
2) ≠0
| x1 | | x2 | | x1(1+x2) | | x2(1+x1) | |
| − |
| = |
| − |
|
|
| 1+x1 | | 1+x2 | | (1+x1)(1+x2) | | (1+x1)(1+x2) | |
| | x1+x1*x2 −x2−x1*x2 | | x1 −x2 | |
= |
| = |
|
|
| | (1+x1)(1+x2) | | (1+x1)(1+x2) | |
licznik z założenia jest rózny od zera więc cały ułamek jest różny od zera więc funkcja jest
różnowartościowa
21 sie 13:15
ania: aa na moim obrazku to max to w 1/3 a nie 0.75
21 sie 13:32
barbaksia: och dziękuję wam serdecznie, że tez człowiek zwlekał tyle lat ze studiami

, a jak wyznaczyć
asymptoty w zadaniu 4?
21 sie 15:55
barbaksia: wzory znam ale cóż

? lim x→
∞ f(x)/x i lim x→
∞ [f(x) − ax]
21 sie 15:57

 wyobraźnie można posiłkować wolframem w razie problemów
http://www.wolframalpha.com/input/?i=x%28x%E2%88%921%29%5E2+%2B1
wyobraźnie można posiłkować wolframem w razie problemów
http://www.wolframalpha.com/input/?i=x%28x%E2%88%921%29%5E2+%2B1

 , a jak wyznaczyć
asymptoty w zadaniu 4?
, a jak wyznaczyć
asymptoty w zadaniu 4?
 ? lim x→∞ f(x)/x i lim x→∞ [f(x) − ax]
? lim x→∞ f(x)/x i lim x→∞ [f(x) − ax]