Układ równań Bajka: Rozwiąż algebraicznie lub graficznie następujący układ równań: y+|x−2|=3 y=|x+2|−1

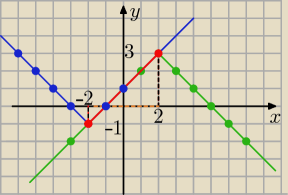
Eta: Metoda graficzna: y = −|x−2|+3 −−−−− wykres zielony y = |x−2|−1 −−−−− wykres niebieski Punkty wspólne obydwu wykresów na czerwonym odcinku na prostej y=x+1 to rozwiązaniem układu równań, są wszystkie punkty (x,y) takie,że: y= x+1 dla x€<−2, 2>

Bajka: A mogę prosić jeszcze o rozwiązanie algebraiczne.

Eta: Spróbuj samodzielnie Podam jedynie wskazówki: y= −|x−2|+3 i y= |x+2| −1 rozpatrz przedziałami 1^o x€ ( −∞, −2) 2^o x€ <−2, 2) 3^o x€ <2,∞) Powodzenia ..... a wynik masz z interpretacji geometrycznej

Eta: Szkoda,że nie znasz słowa dziękuję

Bajka: Zawsze za zrobienie zadań piszę DZIĘKUJĘ

Eta: Hmmm .... a ja tu nie widzę

Bajka: Bo zadanie nie było skończone.

Eta: Logiczne myślenie

Bajka: Zrobiłam te zadanie, ale bardzo proszę o sprawdzenie: |x+2|−1+|x−2|=3 x+2+x−2=4 ∨ −x−2−x+2=4 2x=4 ∨ −2x=4 x=2 ∨ x=−2 y=x=2−1 y=x+1

Aga1.: Źle, musisz rozpatrywać trzy przypadki, wskazówek udzieliła Ci Eta

Bajka: Czy to tak ma być: 1. (−∞,−2) −x−2−x+2=4 −2x=4 x=−2 2. <−2,2) x+2−x+2=4 2x=0 x=0 3. <2,+∞) x+2+x−2=4 2x=4 x=2 y=x+2−1 y=x+1

Aga1.: 1. −2∉(−∞,−2) 2. 0=0 Rozwiązanie x∊<−2,2) 3. 2∊<2,∞) Odp. x∊<−2,2>

Bajka: DZIĘKUJĘ.