f.wykładnicza ja:

	⎧	x gdy x≥0
Dla jakich wartości parametru m∊R równanie (m−3)4	⎨		−2m+1=0 ma dwa
	⎩	−x gdy x<0

różne rozwiązania po 4 jest do potegi wartosci bezwzglednej z x

Bogdan: Czy taki jest zapis równania? (m − 3)*4^|x| + 2m + 1 = 0

Bogdan: jeszcze raz, bo wstawiłem znak plus przed 2m, zamiast minus: (m − 3)*4^|x| − 2m + 1 = 0

pp: tak taki jest zapis

Bogdan: Wobec tego mamy dwa wykresy: y = 4^|x| to zmodyfikowany wykres funkcji wykładniczej i

	2m − 1
y =		to linia prosta równoległa do osi odciętych.
	m − 3

Naszkicuj pierwszy wykres i kilka linii prostych przecinających ten pierwszy wykres w dwóch punktach

Artur_z_miasta_Neptuna:

	2m−1
Bogdan −−− y=		nie jest prostą i to jeszcze równoległą do osi ... w końcu:
	m−3

2m−1		7
	= 2 +
m−3		m−3

Bogdan: Przemyśl Arturze swoją wypowiedź.

	2m − 1
Wykres y =		jest prostą będącą wykresem funkcji stałej z parametrem m,
	m − 3

m jest parametrem!

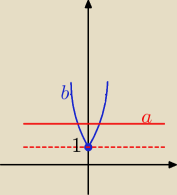
Bogdan: To od początku.

	2m − 1
(m − 3)*4|x| − 2m + 1 = 0 ⇒ 4|x| =
	m − 3

y = 4^|x| (wykres b)

	2m − 1
y =		(wykres a)
	m − 3

Widzimy, że linia a przecina linię b w dwóch punktach wtedy, gdy linia a jest

	2m − 1
nad linią y = 1, stąd zachodzi		> 1 i m ≠ 3
	m − 3

Trzeba rozwiązać ostatnia nierówność.

Bogdan: Arturze − czy zgadzasz się ze mną? (przepraszam za skrócenie twojego nicku)