zadanie Eta: Dla Saizou Witam Widzę,że za bardzo się nudzisz zad.1/ Wykaż,że jeżeli a,b,c są długościami boków trójkąta i R , r odpowiednio długościami promieni okręgu opisanego i okręgu wpisanego w ten trójkąt, to zachodzi równość

	1		1		1		1
		+		+		=
	ab		ac		bc		4Rr

Saizou : Eto witaj i ja się nie nudzę

Eta:

Eta: I jak Saizou? nie masz ochoty na to zadanie?

Saizou :

	1		1		1		1
Teza:		=		+		=
	ab		ac		bc		4Rr

	a+b+c		1
sprowadzając lewą stronę tezy do postaci jednego ułamka otrzymuję:		=
	abc		4Rr

Dowód: −promień okręgu opisanego na trójkącie to

	abc
R=
	4P

	abc
P=
	4R

− promień okręgu wpisanego w trójkąt to

	2P
r=
	a+b+c

	r(a+b+c)
P=
	2

r(a+b+c)		abc
	=
2		4R

4Rr(a+b+c)=2abc

4Rr(a+b+c)
	=1
2abc

a+b+c		1
	=		cnu
abc		2Rr

Tylko mi w tezie nie pasuje ta czwórka w mianowniku

luk20: Ja przyłączam się do Saizou, coś jest nie tak z tą 4...

Eta: No bo chochli narozrabiał

	1		1		1		1
ma być:		=		+		+
	2Rr		ab		ac		bc

Saizou : czyli jest OK

Eta: przecież wykazałeś!

Saizou : myślałem że gdzieś po drodze coś pomyliłem

Saizou : to może jeszcze jakieś jeden dowodzik?

Saizou :

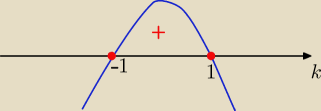
Eta: Zad.2 Wyznacz liczbę rozwiązań równania ||x+1| −1|+k²=1 w zależności od parametru "k"

Saizou : llx+1l−1l=1−k² i tak się zastanawiam że to równanie ma sens tylko dla k²≤1 czyli dla k∊<−1:1>

Eta: zad.3/ Wykaż,że liczba:

	1		1		1
W=		+		+ ......... +
	√1+√4		√4+√7		√97+√100

jest liczbą całkowitą .

Eta: 1−k² ≥0 ⇒ x€ .............

Saizou : x∊R

Eta:

Eta: Nie osłabiaj mnie (1−k)(1+k) ≥0 ⇔ k€ ...........

rumpek: Bry

Saizou : za to mam już dowód zrobiony w moim kajeciku k∊<−1:1>

Eta: Bryyyyy rumpek

Eta: @Saizou zadanie 2/można rozwiązać algebraicznie lub ( szybciej) graficznie

Saizou : wcale nie jest zimno witam rumpka

Eta: Brrrr −− to by było zimno

Saizou : to może narysować sobie funkcje f(x)=llx+1l−1l−1 a następnie badać jak zmienia się funkcja poprzez przesuwanie wykresu względem osi y poprzez k²

Eta: poprzez "y=m" dla m= 1−k²

Saizou : czy to jest w ogóle dobry trop? bo mi wychodzi że dla k∊(−∞:−1)U(1:+∞) jest 0 rozwiązań k∊{−1:1} są 2 rozwiązania k∊(−1:0)U(0:1) są 4 rozwiązania k∊{0} są rozwiązania 3 rozwiązania

Eta: Ok

Saizou : usuwając niewymierność z liczb otrzymamy że

1		1
	=
√1+√4		3

1		−2+√7
	=
√4+√7		3

1		−√7+√10
	=		...
√7+√10		3

1		−√97+10
	=
√97+√100		3

1		−2+√7		−√7+√10		−√97+10		9
	+		+		+...+		=		=3 cnu
3		3		3		3		3

a teraz znika na jakieś 30 minut

Eta:

Saizou : wróciłem

Eta: Coś krótka ta "randka"

rumpek: Saizou jest sprinterem

Eta:

Saizou : w sumie to odcinek trwał 26 minut

rumpek: dobranocka ?

Saizou : nie, anime

rumpek: eee tam, anime pamiętam te czasy jak się czekało na dobranockę typu: http://www.youtube.com/watch?v=rTiSt4ibHBI http://www.youtube.com/watch?v=axJ4ZVEUDyc A nie to co teraz dają w telewizji Ma się sentyment do tych bajek

rumpek: No i jeszcze http://www.youtube.com/watch?v=vENXCSp7Bg0 obowiązkowo

Saizou : ja wolałem Koziołka Matołka a Kubusia też pamiętam przecież to Disney'a a piosenki w tych bajkach są na prawdę świetne

Saizou : kiedyś miałem całą kasetę video nagraną Gumisii zawsze jak się było chorym to siadło się przed Gumisiami

rumpek: ja przed Puchatkiem albo Sąsiadami

Saizou : a pamiętasz Pokemony

rumpek: starałem się tego unikać ale niestety w podstawówce "tazo" się zbierało

Eta: A ja takie http://www.youtube.com/watch?v=vKFeQ8SzZdQ

Saizou : Pierwsza polska bajka

Eta:

rumpek: wilk i zając też była dobrą bają i krecik

Saizou : a kto lubi jabłeczniki? bo znalazłem b. łatwy przepis na jabłecznik

Eta: https://matematykaszkolna.pl/forum/152519.html

Eta: Hehe właśnie wczoraj piekłam

Eta: https://matematykaszkolna.pl/forum/152527.html

rumpek: mi dzisiaj udało się wymodzić sernik z naturalnego sera tj.: nie tego kupnego, tylko tego ręcznie robionego z mleka prosto od krowy

Saizou : http://kotlet.tv/szarlotka-sypana bardzo prosta w przygotowaniu i smaczna

Eta: Łaciatej?

rumpek: tak [nie mylić z łaciatą kartonową − gdzie więcej płacimy za opakowani niż za rozcieńczone mleko ]

Eta: A co robi kotlet? w tej szarlotce?

Saizou : smakuje

Saizou : to co może jakiś dowód, może być geometryczny

Eta: Zaraz rumpek coś Ci "sypnie" Ja na razie idę na ............ herbatkę

Saizou : i na szarlotkę

rumpek: Masz prościutki za 2pkt: (a ⋀ b ⋀ c ⋀ d) > 0 Wykaż, że 4√abcd ≤ (a + b)(c + d) Tyle fajnych dowodów jest z trygonometrii i logarytmów których nie miałeś

Saizou : rumpek w następne wakacje już będą przerobione

Eta: @ rumpek A ja mogę ?

rumpek: ale, że zadanie ? Jak nie będzie wiedział [w co wątpię] to tak i nawet wiem jak to rozwiążesz Eto

Eta: am −gm

rumpek: ciii

Saizou : jak dla mnie wystarczy tylko jedno przekształcenie

	(a+b)(c+d)
0≤
	4√abcd

jeśli a,b,c,d>0 to i(a+b)(c+d) jest zawsze dodatnie, a z definicji pierwiastka kwadratowego mamy że pierwiastek ten musi być zawsze dodatni więc iloraz (a+b)(c+d) oraz 4√abcd jest dodatni ckd

rumpek: z tego co pamiętam to Saizou ostatnio też nie zrobił tego twojego dowodu z tych zależności

Saizou :

Saizou :

Saizou : widzę że rumpek też poszedł na herbatkę i na sernik "prosto od łaciatej"

jaaaa ale spam:

Saizou : z/w

Mila: Oj, niedobrze, niedobrze. ( Saizou)

luk20: a jeśli ja mogę się wtrącić to doszedłem do takiej postaci 0≤(√ac−√bd)²+(√ad−√bc)² ckd

Saizou : a czemu tak nie może być?

Saizou : w końcu jak dzielimy dwie liczby dodatnie to wynik jest zawsze dodatni

Mila: Saizou, podziel dobrze.

Saizou : ale co jest złego w moim dowodzie, bo dla mnie jest OK

tomek: Saizou, jak dzielisz x przez x to zostaje 1 a nie 0

luk20: Jest źle podzielone, po lewej stronie na pewno nie jest 0

Saizou : a 0≤1 zatem jest to prawda

Mila: wynik po podzieleniu:

(a+b)(c+d)
	≥1( a nie 0)
4√abcd

Saizou : luk20 przez zero się nie dzieli

Eta: Ejjj Saizou dałeś "plamę "

rumpek: no to Eta do dzieła

Saizou : mam pomysł dajcie mi jeszcze chwilę

Eta: Hej Mila A już myślałam,że Saizou sam znajdzie błąd

Eta: @ rumpek , a Ty co ? w wojsku "robisz" za dowódcę?

Saizou : 4√abcd≤(a+b)(c+d)

	(a+b)(c+d)
√ac*√cd≤
	4

	a+b		c+d
√ac*√cd≤		*
	2		2

i tu trzeba wykorzystać zależność między śr_geo≤śr_art

Eta: Dokańczaj ..........tak by nie stracić punktu

rumpek: zgodnie z ustawą z godziny 20:40 mówiącej o możliwości podjęcia przez Ciebie, tj.: użytkownika o nicku Eta przedstawieniu pełnego dowodu, po spełnieniu warunku przez Saizou − nie wywiązaniu się z umowy tj.: nie zrobienie zadania, lub błędne jego wykonanie. Post z godziny 20:44 użytkownika Saizou czyni Ciebie spadkobierczynią dowodu. Dlatego pozwoliłem napisać sobie post z godziny 22:01 w celu poinformowania o "zdobyczy". Z poważaniem, rumpek

Eta: Na razie oglądam " Czas Honoru"

Saizou : chochlik w pierwiastku przy a ma być b czyli √ab

	a+b
√ab≤
	2

4ab≤a²+2ab+b² 0≤(a−b)² oraz 2√cd≤c+d 0≤(c−d)² a dalej to brak pomysłu

Eta: Widzę,że zasłużenie zdałeś maturę z j. polskiego

rumpek: Z zależności śr. ar ≥ śr. geo.

⎧	a + b ≥ 2√ab
⎩	c + d ≥ 2√cd

mnożymy stronami (a + b)(c + d) ≥ 4√abcd c.n.u.

rumpek: a dziękuję

Saizou : rumpek ja nic nie podpisywałem

Eta:

	d+c
i √dc≤
	2

i pomnóż obydwie nierówności stronami , co zakończy dowód

Saizou : Eta i setka znowu Twoja

rumpek: Eta ma szczęście do "setek"

luk20: A to do czego ja doszedłem jest dobrze, post z 21:37

Mila: Dla tych, co nie pamiętają o średnich. I na wtorkową maturkę. {√a−√b)²≥0 ⇔a−2√ab+b≥0 {√c−√d)²≥0 ⇔c−2√cd+d≥0 a+b≥2√ab c+d≥2√cd (a+b)(c+d)≥4√abcd

Mila: LUk20 − dobrze, o ile "środek"dobry.

Saizou : ja poproszę jedno zadanko na dobre spanko

miłosz: proponuje abyście mi odpowiedzieli na moje pytanie ↓ https://matematykaszkolna.pl/forum/152430.html

Mila: Dla Saizou: Rozłóż na ułamki proste:

	8
	9

Saizou :

8		1		1		1
	=		+		+
9		2		3		18