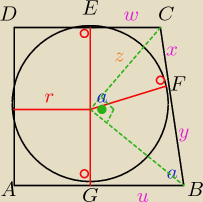
trapez prostokątny Krzychu: Dany jest trapez prostokątny o kącie ostrym α. Promień koła wpisanego w ten trapez jest równy r. Oblicz obwód trapezu.

α
	=β
2

ΔOFC

	x
tgβ=
	r

x=rtgβ ΔOFB

	r
tgβ
	y

y=rtg CB=x+y=2rtgβ ΔOEC

	w
tgβ=
	r

w=rtgβ ΔOBG

	r
tgβ=
	u

u=rtgβ Obw=4r+x+y+w+u=4r+4rtgβ Dobrze?

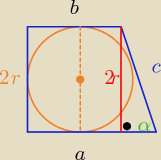
Eta: Krzychu nie utrudniaj sobie życia h=2r z warunku opisania trapezu na okręgu: a+b= 2r+c

	h		2r
Ob= a+b+2r+c = 4r+2c ,		= sinα ⇒ c=
	c		sinα

	2r		1
Ob= 4r+2*		= 4r(1+		)
	sinα		sinα

Mila: Wcześniej pisałam Ci własność o odległości punktów styczność od wierzchołków kąta: stąd u=y i x=w W ΔOFB:

	r
tgβ=		/*y
	y

y*tgβ=r

	r
y=		=r*ctgβ
	tgβ

	α		α
x+y=r tg		+r ctg
	2		2

Mila: Witaj Eto!

Eta: Witaj Mila

Krzychu: A zapomniałem o tym warunku a+b=c+d

	α		α
w obliczeniach się pomyliłem, a odpowiedź Ob=4r+2rtg		+2rctg		jest ok ?
	2		2