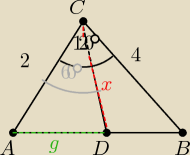
mam tu takie oo KEK: w trojkacie abc dlugosci bokow ac i bc sa odpowiednio rowne 2 i 4 zas miara kata acb wynosi 120 oblicz dlugosc odcinka ktory jest czescia wspolna dwusiecznej kata acb i trojkata abc robilem tak: trzeci bok AB = c dwusieczna przecina AB w punkcie D z tw kosinusa wyszedl c 2√7, potem licze AD z tw dwusiecznej 2/g=4/2{7}−g. wyszlo g=4√7/6 z tw kosinusa licze CD powstaje row, kwadratowe i wychodza 2 wyniki 2/3 i 4/3 a w odpowiedzi jest tylko 4/3 prosze o jakies info dlaczego odrzucamy wynik 2/3

Artur_z_miasta_Neptuna: skoro masz AD wyznaczony ... to CD = c − AD

Artur_z_miasta_Neptuna:

Artur_z_miasta_Neptuna: więc coś masz nie teges

KEK: g²=2²+x²−2*2*x*cos60 sprawdzalem jeszcze raz i to samo 2 wyniki 4/3 i 2/3, a w odpowiedziach jest tylko 4/3...

Bogdan: Wynik jest jeden.

	4
x =
	3

KEK:

	4√7
(		)2=22+x2−2*2*x*(cos60)
	6

112		1
	=4+x2−4x*(		) //*36
36		2

112=144+36x²−72x 36x²−72x+32=0 Δ=5184−4608=576=24² Δ>0

	72−24
x1=		=23
	72

	72+24
x2=		=43
	72

dwa.

Artur_z_miasta_Neptuna:

	2
g =		√7
	3

	4
czyli c−g =		√7
	3

	4		8
jeżeli tutaj zastosujesz tw. cosinusów to wyjdzie x=		lub x=
	3		3

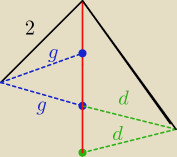
Artur_z_miasta_Neptuna: dlaczego otóż patrz rysunek (d = c−g) wyniki dwa wychodzą w obu przypadkach, ponieważ bok g (d) może być na dwa sposoby 'ustawiony'

Artur_z_miasta_Neptuna: zmienią się pozostały dwa kąty i długość 'x' ... ale dlugość boków 'danych' (wyliczonych) będzie taka sama.

Bogdan:

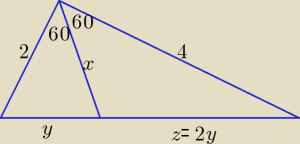
	y		z
Z twierdzenia o dwusiecznej w trójkącie:		=		⇒ z = 2y
	2		4

Z twierdzenia cosinusów (cos60^o = 0,5, cos120^o = −0,5): y² = x² + 4 − 2x 4y² = x² + 16 − 4x Stąd 3y² = −2x + 12

	28
Z tw. cosinusów: 9y2 = 4 + 16 + 8 = 28 ⇒ 3y2 =
	3

	28		8		4
Mamy więc:		= −2x + 12 ⇒ 2x =		⇒ x =
	3		3		3

tak: ∫443⇒3

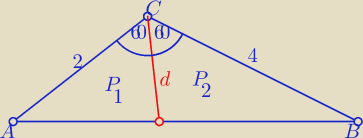
Eta: A tak przy okazji taki sposób :

	1
PΔABC=		*2*4*sin120o ⇒ P=2√3
	2

P=P₁+P₂

	1		d√3
P1=		*2*d*sin60o ⇒ P1=
	2		2

	1		2d√3
P2=		*4*d*sin60o ⇒ P2=
	2		2

	3d√3
P1+P2=P ⇒		= 2√3
	2

	4
d=
	3

=======