g jaa: dane sa rownania dwoch okregow: (x−3)²+y²=9 i (x+5)²+y²=25. znajdz rownania prostych stycznym do obu tych okregow

Klara: Pomagam Cierpliwości narysuję te okręgi.

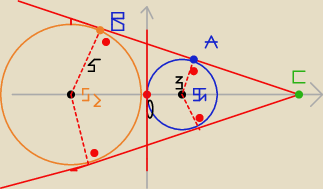Klara: okrąg (x −3)² +y² = 9 S₁( 3,0) r₁= 3 okrag: ( x+5)² +y²= 25 S₂(−5,0) r₂= 5 obydwa okręgi są zewnętrznie styczne w punkcie O(0,0) więc mają trzy styczne: 1 styczna to prosta o równaniu x =0 −−−−−− zawiera punkt(0,0) pozostałe dwie styczne są symetryczne względem osi OX zatem mają równania: styczna CB : y = −ax +b gdzie a = tgα α= <CS₂B =<CS₁A ponieważ współczynnik kierunkowy stycznej BC równy jest tgα , gdzie kąt α −−− jest kątem nachylenia tej prostej do dodatniej osi OX czyli tg(180^o −α) = − tgα= −a tgα=UIACI}{IS₁AI} zatem : IS₁AI= 3 ΔCS₁A~ΔCS₂B więc:

ICS1I		ICS2I
	=
IS1AI		IS2BI

	ICS1I		8+ICS1I
to:		=
	3		5

to: 5ICS₁I= 24 +3ICS₁I => ICS₁I= 12 to punkt C( 12+3, 0) czyli C(15,0) zatem z ΔCS₁A z tw. Pitagorasa obliczymy: IACI = √IS₁CI² − IAS₁I² => IACI= √144 − 9 to IACI = √135 = 3√15

	IS1AI
więc już mozemy wyliczyć tgα=
	IACI

	3
tgα=		=> tgα=√1515
	3√15

to a = − ^√15₁₅ zatem pozostałe styczne mają równanie: styczna BC: y = −^√15₁₅*x +b i C€ do tej stycznej więc 0= ^√15₁₅*15 +b => b = √15 zatem styczna BC: y = −^√15₁₅x +√15 to styczna B^'C : y= ^√15₁₅*x −√15 Myślę ,że się nie pomyliłam w rachunkach , ...... sprawdzaj