Jak zaznaczyć na osi zbiór rozwiązań wartości bezwzględnej?
Edyta: Korzystając z interpretacji geometrycznej wartości bezwzględnej, zaznacz na osi liczbowej
zbiory liczb opisanych poniższymi warunkami.
a) |x|=1
b) |x| > 4
c) |x| ≤ 5
d) | x + 3 | = 4
e) | x − 1 | ≥ 2
f) | x + 5 | < 3
g) | 3 − x | > 6
h) | x − 2 | ≥ 1
16 sie 13:06
picia:
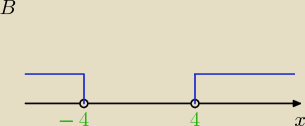
16 sie 13:16
loitzl9006: Wyrażenie |x−a| określa odległość od punktu a (na osi x). Np. |x−1| określa odległość od punktu
1.
Załóżmy, że mamy coś takiego:
|x−1|=2
Jakie punkty spełniają to równanie? Wszystkie takie, które są oddalone o dwie jednostki od
punktu 1.
|x+1|=2
Wszystkie punkty oddalone o dwie jednostki od punktu −1.
| x + 5 | < 3
Wszystkie punkty oddalone o mniej niż trzy jednostki od punktu −5.
w g) wykorzystaj, że |3−x| = |x−3|. Skąd ta własność? Stąd, że |a|=|−a| dla każdej rzeczywistej
liczby a. np. |−4|=|4|.
16 sie 13:43
Mila:
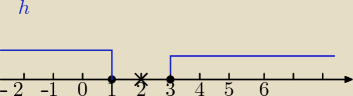
h) | x − 2 | ≥ 1
16 sie 16:14
asdsad: γβα
12 mar 18:18

 h) | x − 2 | ≥ 1
h) | x − 2 | ≥ 1