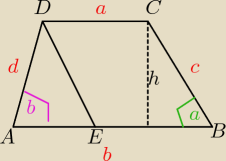
Trapez denatlu: Podstawy trapezu mają długość a,b (a>b), a kąty ostre trapezu to α i β. Oblicz pole tego trapezu. P=^(a+b)h₂ Jak wyliczyć tutaj h? Albo może coś innego? Można prosić o jakąś wskazówkę?

Artur z miasta Neptuna: zamieniłeś a z b na rysunku....piszę tak jak jest na rysunku.

	bβ
ctgβ =		⇒ h*ctgβ = bβ
	h

	bα
ctgα =		⇒ h*ctgα = bα
	h

	a−b
b = a+ bα+bβ = a+ h(ctgβ+ctgα) ⇔ h =
	ctgβ+ctgα

	(a+b)h		(a+b)(a−b)		a2−b2
Pole =		=		=
	2		2(ctgβ+ctgα)		2(ctgβ+ctgα)

Artur z miasta Neptuna: no i pierdyknąłem się w drugiej i trzeciej linijce ... b−a w liczniku powinno być

denatlu: co to jest b_β, b_α ?

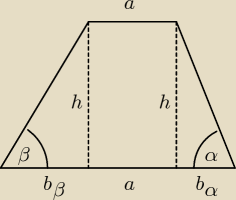
Artur z miasta Neptuna: dlatego b = a + b_α + b_β

denatlu: pierwszy raz z takim zapisem się spotkałem, dlatego pytam. Dzięki. A masz jakiś pomysł, jak zapisać to przy pomocy sinusów? Bo w książce mam właśnie taką odpowiedź po zrobieniu tego równoległoboku.

Artur z miasta Neptuna: a długości ramion są dane czy nie

Mila:

	cosα
ctgα=
	sinα

	cosβ
ctgβ=		podstawić i przekształcic.
	sinβ