zadania [P[Milowe]] Saizou : pytania: http://www.zadania.info/d5/49438 odpowiedzi moje: http://img215.imageshack.us/img215/5951/matematykaj.jpg jak by ktoś się nie mógł doczytać to proszę pisać

Bogdan: Zad. 4 bez Δ Jesli 0 ≥ −4n² + 4n − 1, to 4n² − 4n + 1 ≥ 0 ⇒ (2n − 1)² ≥ 0

Saizou : na ten pomysł wpadłem jak policzyłem deltę

Saizou : są jakieś błędy?

Mila: Rozwiązuję i sprawdzam po kolei. Uwagi po skończonej pracy. Wielki bałagan w zapisie.

Saizou : to jest matematyczny nieład

Eta: taaaakie bazgroły

Mila: zadanie 1− dobrze, zapisy uporządkować. zadanie 2− dobrze zadanie 3 Mogłeś rozważyć tylko 2 przypadki: y≥−2 y<−2 Spróbuj zrobić na forum, może się innym też przydac. zadanie 4 − uwaga Bogdana zadanie 5.−dobrze byłoby zestawić wszystkie wartości w tabelce, mniej miejsza zajmuje i łatwiej odczytac . zadanie 6,8,9 dobrze Nie widzę 7,10,11.

Eta: Zad4/ w końcówce: −4n²+4n −1 ≤0 /*(−1) 4n²−4n+1≥0 (2n−1)²≥0 c.n.u

Eta: Zad.7/ ? ( łatwe

rumpek: może inaczej w zasadzie nie ma tutaj żadnego trudnego zadania

Mila: Rumpek, to zadania dla uczniów po I klasie LO. Uważam, (z doświadczenia)że nie są banalne dla uczniów klasy I.

Eta: dla Mili a dla rumpka <figa>

Saizou : Mila zadaniu 5 było trzeba narysować wykres

rumpek: widzę, że sezon na jabłka się skończył

Eta:

Mila: Saizou. W zadaniu 5 − wykres dobry, ale obliczenia mogłeś zrobić w tabeli. Rumpek, figa od Ety, to objaw sympatii.

Saizou : ale przecież to takie proste obliczenia

rumpek: Saizou masz takie proste: Wykaż, że 8ⁿ + 6 | 7, n∊N₊

Saizou : a co oznacza ta kreska pionowa?

rumpek: podzielne

rumpek: Wykaż, że 7 | 8ⁿ + 6, n∊N₊

rumpek: no i w nawiasie xD

Saizou : czyli co mam wykazać, bo się zgubiłem

Eta:

rumpek: Wykaż, że 7 | (8ⁿ + 6); n∊N₊ ("|" − oznacza podzielność) Napisałbym ładnie z kwantyfikatorem ale niestety forum nie obsługuje

Eta: 7| (8ⁿ+6) dla n€N+

Eta: ∀

Saizou : może jakaś podpowiedź

rumpek: indukcja

Mila: Dwumian Newtona.

rumpek: kongruencje

Godzio: 8ⁿ + 6 = 7 * 8ⁿ − 6 * 8ⁿ + 6 = 7 * 8ⁿ − 6(8ⁿ − 1) = 7 * 8ⁿ − 6(8 − 1)(8^{n − 1} + 8^{n − 2} + ... + 1) = 7 * (8ⁿ − 6(8^{n − 1} + 8^{n − 2} + ... + 1) ) c.n.d Bez tych waszych pomysłów

Eta: aⁿ−1= (a−1)(aⁿ⁻¹+aⁿ⁻²+... +1) 8ⁿ+6 = (8ⁿ−1)+7 Teraz działaj

Eta: Wrrrrrrrrrrr

Godzio:

Eta:

Godzio: Jestem chory i zdrowieje przy matematyce i herbatce

Eta: @Saizou Ja wciąż czekam na zad. 7

Godzio: To 7 jest tak banalne, że wstyd je robić

Eta: ja też piję herbatkę z pigwą

Eta: Godzio Zaraz Ci wrzucę link, jak się nad nim męczyłeś ( swego czasu)

Godzio: http://fotoforum.gazeta.pl/photo/4/ej/hf/d89a/0FHady2El8xqd2j0pX.jpg Pora poprawić sobie samopoczucie

Godzio:

Eta:

Godzio: Stare dobre czasy, jak się jeszcze fali nie umiało rysować

Eta: Bo Jakub nie wrzucił "fali" w opcji rysowania

Godzio: Pewnie dlatego

Godzio: Niezła zabawa u Ety

Eta:

rumpek: To przez pigwę

Godzio: Ja już lecę spać, rano trzeba wstać Dobranoc

rumpek: Pracuś

Eta:

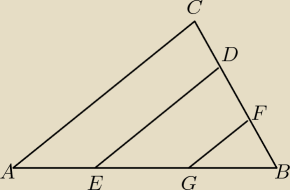
Saizou : zadania 7 jeśli pola są równe to można zapisać że

	1
PBFG=		PABC
	3

	2
PBDE=		PABC
	3

są to trójkąty podobne do trójkąta ABC zatem mogę zapisać że:

	1   PABC 3
k2=
	PABC

	1
k=√
	3

oraz że

	2   PABC 3
k2=
	PABC

	2
k=√
	3

zatem można zapisać że

	1		√3
BG=√		a=		a
	3		3

	2		√6
BE=√		a=		a
	3		3

	√6		√3		√6−√3
EG=		a−		a=		a
	3		3		3

	√6		3−√6
AE=a−		a=		a
	3		3

Bogdan: Rozwiązanie zadania 7 jest błędne. Nie istnieje k = √1/3 i jednocześnie k = √2/3.

Saizou : fakt miało być k₁ i k₂

Bogdan: Zostały jeszcze dwa zadania

Saizou :

	→		→		→
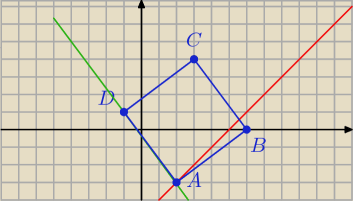
wiedząc że wektor		=[4;3]=		mogę wywnioskować że wektor		=[−4:−3].
	AB		DC		CD

Wiedząc że punkt A leży na prostej x−y=5, mogę go wyznaczyć ze pomocą prostej prostopadłej do odcinka DC przechodzącej przez punkt D, zatem punkt A=(2:−3), zatem punkt B=(6:0). zatem prosta przechodząca przez punkty C i D ma wzór: 4=3a+b −3=2a+b a=7 b=−17 zatem wór przekątnej to y=7x−17

	6
obliczamy również prostą zawierającą punkty B i D, i wzór tej prostej to y=U−{1}{7}x+
	7

Saizou : zostało zadanie znienawidzone przeze mnie, zadania z wiekiem

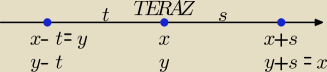
Bogdan: Zadanie nr 10. Ktoś zapytał znajomego „Ile masz lat?”. „Teraz mam dwa razy więcej niż ty miałeś gdy ja byłem w twoim wieku. Gdy ty będziesz w moim wieku, razem będziemy mieć 63 lata”. Ile lat ma każdy z nich obecnie? W gruncie rzeczy to łatwe zadanie. Szkicujemy oś czasu i wprowadzamy na rysunek dane podane w zadaniu. Przyjmuję oznaczenia: x − teraz ja mam tyle lat, y − teraz ty masz tyle lat, t − liczba lat w przeszłość s − liczba lat w przyszłość x − t = y i x = 2(y − t) ⇒ t = x − y i x = 2y − 2x + 2y ⇒ 3x = 4y oraz y + s = x i x + s + y + s = 63 ⇒ s = x − y i x + y + 2x − 2y = 63 ⇒ 3x − y = 63 Stąd 4y − y = 63 ⇒ y = 21 i 3x = 4*21 ⇒ x = 28 Odp.: Teraz ja mam 28 lat, ty 21 lat,

picia: Genialne!

Saizou : ale ja nigdy nie lubiłem zadań z wiekiem

Bogdan: A kogo z układających arkusz maturalny obchodzi, co kto lubi? Trzeba zrobić ile się da i to dobrze, bez grymaszenia: lubię, nie lubię.

Saizou : nie lubię