Ale cisza jak makiem zasiał
Saizou : to może jakieś zadanko ale nie optymalizacyjne

10 sie 22:40
Basia: a dwumian Newtona już sobie przerobiłeś ?
mam takie zadanka pod ręką

10 sie 22:53
Godzio: A moje zadanie zrobione

? (to z środkowymi)
10 sie 22:56
Saizou : 
poziom I LO
10 sie 22:56
Saizou : wyleciało mi z głowy że mam je zrobić, już go szukam

10 sie 22:58
rumpek: poziom 1 LO czyli logika była

?
Godzio z tego co pamiętam miałeś zacząć studia na UWr
w tym roku

?
10 sie 22:59
Saizou : Wyznacz długości boków a,b,c trójkąta mająca dane środkowe: s1,s2,s3.
10 sie 22:59
Godzio: Napisze

Wyznacz długość środkowych, s
1, s
2, s
3 trójkąta o bokach długości: a, b i c
Wystarczy, że mi jedną wyznaczysz, reszta idzie na jedno kopyto

10 sie 23:00
Godzio: No bez różnicy, w którą stronę, czy środkowe czy boki
 rumpek
rumpek owszem, zaczynam

10 sie 23:01
rumpek: Informatyka

?
10 sie 23:01
Godzio: Matematyka, no co Ty

10 sie 23:01
rumpek: to się z
TOmkiem spotkasz

10 sie 23:02
Godzio:
Tak

? Spoko

10 sie 23:03
rumpek: tak

10 sie 23:04
10 sie 23:07
rumpek: Basiu można było podać inną stronę

[bo tam jest już udowodnione]

10 sie 23:08
Basia:
a musi
Saizou podglądać ?
jeżeli sobie sam nie poradzi wtedy może podejrzeć

10 sie 23:10
Saizou :
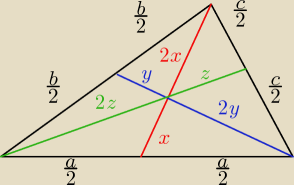
jak na razie to mam rysunek zrobiony no i myślę że z wzoru Herona można by skorzystać?
10 sie 23:12
Godzio:
A miałeś np. twierdzenie sinusów/cosinusów ?
10 sie 23:13
Basia:
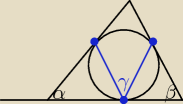
10 sie 23:14
rumpek: pamiętam te czasy, jak
Godzio męczył mnie tym zadaniem

10 sie 23:14
Saizou : tw. cosinusów umiem
10 sie 23:15
rumpek:

Wyznacz kąty dalej już łatwo idzie

akurat kąty umiesz wyznaczyć

10 sie 23:21
Godzio:
No to jak umiesz, to zadanie jest banalne

10 sie 23:22
Godzio:
Pamiętam jak się męczyłeś nad łatwiejszymi zadaniami, a teraz lepszy ode mnie jesteś

10 sie 23:22
rumpek: wątpię

10 sie 23:24
Godzio: A ja nie

Trochę się rozleniwiłem przez te studia

10 sie 23:24
Saizou : a
2=b
2+c
2−2bc*cosα
a
2−b
2−c
2=−2bc*cosα
analogicznie dla dwóch pozostałych kątów otrzymujemy, że
10 sie 23:27
rumpek: no i
Saizou już widzisz dalej jak to zrobić

? [wyników nie sprawdzałem]
10 sie 23:29
Eta* :
Bardziej "elegancko"

10 sie 23:31
Saizou : i dalej tw. cosinusów będę mógł zastosować, aby obliczyć środkowe?

10 sie 23:31
Godzio:

10 sie 23:32
Saizou : | | √2a2−2b2−c2 | |
czyli środkowa z punktu C ma długość |
| |
| | 2 | |
10 sie 23:49
Basia:
z innej beczki:
dla jakich wartości parametru k funkcja
a) f(x) = k*cosx + 2|sinx|
b) f(x) = cosx + k*sinx
jest parzysta
10 sie 23:50
Saizou : aż tak to ja trygonometrii nie umiem
10 sie 23:52
Basia:
tylko wzory redukcyjne są tu potrzebne
cos(−x) = cosx
sin(−x) = −sinx
10 sie 23:54
Saizou : Basiu z moją raczkującą trygonometrią nawet tego nie potrafię zrobić, wrócimy do tego
zadania jak przerobię trygonometrie w szkole, dobrze?
10 sie 23:56
Basia:
pokażę Ci (b)
(a) jest łatwiejsze
(b)
f jest parzysta ⇔
dla każdego x∊R f(−x) = f(x) ⇔
dla każdego x∊R cos(−x)+k*sin(−x) = cosx+k*sinx ⇔
dla każdego x∊R cosx − k*sinx = cosx + k*sinx ⇔
dla każdego x∊R 2k*sinx = 0 ⇔ k=0
10 sie 23:58
Basia:
no to udowodnij, że iloczyn dwóch funkcji parzystych (lub dwóch funkcji nieparzystych)
jest funkcją parzystą
11 sie 00:00
Saizou : zakres funkcji parzystych i nie parzystych wyszedł z liceum
11 sie 00:00
Mila: Saizou, zacznij chodzić wieczorami na randki. Zostaw już zadania.
11 sie 00:02
Saizou : Mila ale ja kocham matematykę

, ale czasami mi nie wychodzi

11 sie 00:03
Mila: Saizou, jesteś w porządku. Zadania lepiej rozwiązujesz niż niektórzy trzecioklasiści.

11 sie 00:09
rumpek: Saizou już wszedł zakres funkcji parzystych razem z pochodnymi i całkami do liceum

dla
rocznika 2012/2013 i późniejszych

11 sie 00:10
Saizou : ale jeszcze wielu rzeczy nie potrafię zrobić, no ale jeszcze przede mną 2 lata nauki w LO więc
mam czas
11 sie 00:11
Saizou : no niestety ale ja zaczynałem naukę w roku 2011
11 sie 00:11
Saizou : Mówię wszystkim Dobranoc

11 sie 00:20
pigor: ...
wyznacz długość środkowych, s1, s2, s3 trójkąta o bokach długości a, b, c.
zdaje mi się, że coś jest nie tak ze znakiem w rozwiązaniu powyżej , dlatego
wyznaczę
s3 (z wierzchołka C) jeszcze raz np. niech
ΔABC −dany trójkąt o |∡BAC|=α i
|CD|= s3= ? − długość tej środkowej,
to stosując 2 razy tw. cosinusów względem kąta α :
a
2= b
2+c
2−2bc cosα i s
32= b
2+
14c−2b*
12c cosα ⇔ 2bc cosα= b
2+c
2−a
2 i
i 4s
32= 4b
2+c
2−4bc cosα ⇒ (2s
3)
2= 4b
2+c
2−2(b
2+c
2−a
2) ⇔
⇔ (2s
3)
2= 2a
2+2b
2−c
2 ⇒
s3=12√2a2+2b2−c2 , a stąd przez analogię
s2= 12√2a2+2c2−b2 oraz
s1= 12√2b2+2c2−a2.

11 sie 11:49
Mila:
Saizou, przesyłam Ci adres "maturki" stosownej dla drugoklasisty ( po wakacjach).
Zarezerwuj sobie czas i zrób wszystko, co potrafisz − podaj czas.
Znajdziesz klucz, to sam sprawdzisz albo podasz na forum problemy.
http://www.zadania.info/d5/49438
Powodzenia
Lubelska OKE przygotowuje bardzo dobre sprawdziany.
11 sie 15:08
Saizou : rzuciłem tylko okiem i pomyślimy co da się zrobić, niektóre te zadania nie są trudne

to może
w poniedziałek je zrobię
11 sie 15:56
Saizou : to może jakieś zadanko

11 sie 22:10
Godzio: Wykazać, że dla dowolnej liczby naturalnej n liczba
| 1 | | 1 | | 1 | | 1 | |
| n4 + |
| n3 − |
| n2 − |
| n |
| 4 | | 2 | | 4 | | 2 | |
jest podzielna przez 6.
11 sie 22:25
miłosz: 14n4+14+12n3+12−14n2+1−12n+12=6k
11 sie 22:38
miłosz: dobrze?
11 sie 22:39
Saizou : | n4 | | n3 | | n2 | | n | | n4−n2+2n3−2n | | n2(n2−1)+2n(n2−1) | |
| + |
| − |
| − |
| = |
| = |
| =
|
| 4 | | 2 | | 4 | | 2 | | 4 | | 4 | |
| (n2+2n)(n2−1) | | (n−1)n(n+1)(n+2) | |
| = |
|
|
| 4 | | 4 | |
(n−1)n(n+1)(n+2) jest to iloczyn czterech kolejnych liczb całkowitych z których jedna jest na
pewno podzielna przez 3 i jedna na pewno podzielna przez 2 i jedna na pewno podzielna przez 4
| | 1 | | 1 | | 1 | | 1 | |
zatem liczba w postaci |
| n4+ |
| n3− |
| n2− |
| n jest podzielna przez 4*6 |
| | 4 | | 2 | | 4 | | 2 | |
zatem liczba
(n−1)n(n+1)(n+2) jest podzielna przez 6
11 sie 22:41
Godzio:
Przeczytaj to co napisałeś

Ogólnie jest ok, ale komentarz ...

11 sie 22:43
Saizou : a co jest nie tak?
11 sie 22:45
Eta* :
Komentarz

11 sie 22:48
Godzio:
Dla n = 2, liczba jest podzielna przez 4 * 6

?
11 sie 22:48
Saizou : podstawiając za n=2, otrzymamy
1*2*3*4=6*4
11 sie 22:50
Saizou : 
11 sie 22:57
11 sie 22:57
Basia:
chodzi o to, że przestawiłeś w komentarzu wyrażenia
(n−1)*n*(n+1)*(n+2) jest podzielne przez 4*6 zatem
| 1 | |
| n4+..... jest podzielny przez 6 |
| 4 | |
11 sie 22:57
Saizou : czyli zmienić tylko koniec że ta liczba jest podzielna przez 6
11 sie 22:58
Basia:
nie; komentarz powinien wyglądać mniej więcej tak:
(n−1)n(n+1)(n+2) jest to iloczyn czterech kolejnych liczb naturalnych z których jedna jest na
pewno podzielna przez 3 i jedna na pewno podzielna przez 2 i jedna na pewno podzielna przez 4
zatem liczba (n−1)n(n+1)(n+2) jest podzielna przez 2*3*4 = 4*6
a stąd wynika, że
| 1 | | 1 | | 1 | | 1 | | (n−1)n(n+1)(n+2) | |
| n4+ |
| n3 − |
| n2 − |
| n = |
| jest podzielna przez 6 |
| 4 | | 2 | | 4 | | 2 | | 4 | |
11 sie 23:05
Saizou : dziękuję bardzo

a teraz panie i panowie wybaczą ale idę pograć w staromodną grę "ZAX the
alien hunter" , którą wygrzebałem dzisiaj z mojej półki z płytami

11 sie 23:07
Eta* :
Miłej zabawy

11 sie 23:12
Mila: Saizou, zawsze grzeczny, jak przystało na przyszłego matematyka.
12 sie 00:00
Saizou : Mila nie zamierzam zostać matematykiem tylko architektem

i może jakieś zadanko

12 sie 19:32
Eta:
No to zadanko dla przyszłego architekta

1/ Wykaż,że dla liczb x,y,y>0 takich ,że x+y+z=1
zachodzi nierówność
| | 1 | |
|
| (1−x)(1−y)(1−z) ≥ xyz |
| | 8 | |
12 sie 19:40
Eta:
2/ W trójkąt równoramienny o bokach długości 13, 13, 10 wpisano okrąg.
Oblicz długość odcinka łączącego punkty styczności okręgu z ramionami trójkąta,
12 sie 19:43
Saizou : Eto trochę wolniej wrzucaj te zadania

12 sie 19:44
Eta:
3/ Oblicz pole trójkąta opisanego na okręgu o promieniu długości r, jeżeli miary
kątów tego trójkąta wynoszą α , β, γ
12 sie 19:45
Eta:
Na razie robię przerwę w "rzucaniu"

12 sie 19:46
Saizou : zrobię je później bo spać mi się zbytnio chce, w ogóle to dzisiaj jakiś senny dzień mam
12 sie 20:14
Eta:
Ja dziś podobnie mam

12 sie 20:19
Mila: Saizou, gratuluję wyboru zawodu. Architekci, to arystokracja biur projektów.
12 sie 20:33
Saizou :
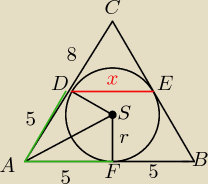
zadanie 2
wiedząc że wysokość w trójkącie równoramiennym dzieli podstawę na dwie równe część mogę zapisać
że AF=BF=5 , jest również dwusieczną kąta pomiędzy ramionami. Z twierdzenia o stycznych okręgu
otrzymujemy że AF=AD=5, zatem odcinek CD=8 bo AC=13. Licząc skalę podobieństwa trójkątów ABC i
CDE (trójkąty są podobne na zasadzie kkk, bo DE jest równoległe do AB) można zapisać że
| | 13 | | 8 | | 2 | |
|
| = |
| , wówczas x=6 |
| |
| | 10 | | x | | 13 | |
12 sie 22:31
Saizou : "Arystokracja" ja się do niej nie zaliczam i na stan dzisiejszy cieszę się że fizyka mi się do
rekrutacji na studia nie liczy

12 sie 22:33
Eta:

Zostały jeszcze dwa zadania

12 sie 23:08
Saizou : na pierwsze na razie nie mam pomysłu, kombinuję coś z trzecim
12 sie 23:21
Saizou : reszta na jutro bo zbyt mi się chce spać

dobranoc wszystkim
12 sie 23:46
Eta:


12 sie 23:48
rumpek: i jak tam postęp

?
15 sie 15:31
Eta:
Nie widać

15 sie 17:35
rumpek: wakacje zaczął

15 sie 17:47
Mila: Poszedł na randkę.

15 sie 17:48
Eta:

15 sie 18:12
rumpek: z matematyką

15 sie 18:16
Saizou : 
nie ładnie obgadywać kogoś

15 sie 18:20
Eta:

"o wilku mowa"

15 sie 18:21
Mila: Przecież sympatycznie.

15 sie 18:21
Saizou : mam jeszcze 30 minut na zadania Mili z OKE Lubelskiej
15 sie 18:22
Eta:
Zobaczcie na forum pojawił się "marzyciel o dużej kasie "

15 sie 18:22
rumpek: Saizou obgadywanie jest wtedy gdzie nie wiesz o tym

Natomiast tutaj masz ładnie
napisane, czarno na białym


15 sie 18:23
Saizou : no może nie czarno na biały, tylko czarno na (no właśnie jaki to kolor)

15 sie 18:26
Eta:
U mnie
szary 
15 sie 18:27
rumpek: w RGB to #e6ddc5

15 sie 18:27
Saizou : u mnie to nie jest szaty

moja siostra określiła to jako beżowy połączony z kawą i mlekiem
15 sie 18:28
Saizou : *szary , można jaśniej
15 sie 18:28
Eta:
Moja
100 
15 sie 18:29
rumpek: Naczy #e6ddc5 jest w hexie, w RGB to: 230, 221, 197

15 sie 18:30
Saizou : no to skończył mi się czas a nie zrobiłem 3 zadań

zaraz wrzucę skany moich obliczeń ale to
już w nowym poście
15 sie 18:53
Saizou : post= temat= wątek
15 sie 18:53
Eta:
Dawaj, dawaj , bo niedługo matura

15 sie 18:55
Saizou : za 2 lata
15 sie 18:56
Eta:
To już......... niedługo

15 sie 18:56
Saizou : jeszcze 2 lata nauki

15 sie 19:00
rumpek: Saizou jakie 2 lata

Policz dobrze

15 sie 19:01
Saizou : jeszcze cała druga klasa i trzecia

15 sie 19:09
rumpek: 2 lata to to nie są

bo za dwa lata o tej porze będziesz miał wolne

15 sie 19:11
Saizou : ja liczyłem systemem nauki w szkole więc 2 lata

15 sie 19:13
rumpek: system nauki szkolnej jest chory

15 sie 19:13
Saizou : i z tym się zgadzam

15 sie 19:15


 ? (to z środkowymi)
? (to z środkowymi)
 poziom I LO
poziom I LO

 ? Godzio z tego co pamiętam miałeś zacząć studia na UWr
w tym roku
? Godzio z tego co pamiętam miałeś zacząć studia na UWr
w tym roku  ?
?
 Wyznacz długość środkowych, s1, s2, s3 trójkąta o bokach długości: a, b i c
Wystarczy, że mi jedną wyznaczysz, reszta idzie na jedno kopyto
Wyznacz długość środkowych, s1, s2, s3 trójkąta o bokach długości: a, b i c
Wystarczy, że mi jedną wyznaczysz, reszta idzie na jedno kopyto 
 rumpek owszem, zaczynam
rumpek owszem, zaczynam 
 ?
?


 ? Spoko
? Spoko 

 [bo tam jest już udowodnione]
[bo tam jest już udowodnione] 

 jak na razie to mam rysunek zrobiony no i myślę że z wzoru Herona można by skorzystać?
jak na razie to mam rysunek zrobiony no i myślę że z wzoru Herona można by skorzystać?


 Wyznacz kąty dalej już łatwo idzie
Wyznacz kąty dalej już łatwo idzie  akurat kąty umiesz wyznaczyć
akurat kąty umiesz wyznaczyć 



 Trochę się rozleniwiłem przez te studia
Trochę się rozleniwiłem przez te studia 
 ? [wyników nie sprawdzałem]
? [wyników nie sprawdzałem]



 , ale czasami mi nie wychodzi
, ale czasami mi nie wychodzi 

 dla
rocznika 2012/2013 i późniejszych
dla
rocznika 2012/2013 i późniejszych 


 to może
w poniedziałek je zrobię
to może
w poniedziałek je zrobię

 Ogólnie jest ok, ale komentarz ...
Ogólnie jest ok, ale komentarz ... 

 ?
?

 a teraz panie i panowie wybaczą ale idę pograć w staromodną grę "ZAX the
alien hunter" , którą wygrzebałem dzisiaj z mojej półki z płytami
a teraz panie i panowie wybaczą ale idę pograć w staromodną grę "ZAX the
alien hunter" , którą wygrzebałem dzisiaj z mojej półki z płytami 

 i może jakieś zadanko
i może jakieś zadanko 
 1/ Wykaż,że dla liczb x,y,y>0 takich ,że x+y+z=1
zachodzi nierówność
1/ Wykaż,że dla liczb x,y,y>0 takich ,że x+y+z=1
zachodzi nierówność



 zadanie 2
wiedząc że wysokość w trójkącie równoramiennym dzieli podstawę na dwie równe część mogę zapisać
że AF=BF=5 , jest również dwusieczną kąta pomiędzy ramionami. Z twierdzenia o stycznych okręgu
otrzymujemy że AF=AD=5, zatem odcinek CD=8 bo AC=13. Licząc skalę podobieństwa trójkątów ABC i
CDE (trójkąty są podobne na zasadzie kkk, bo DE jest równoległe do AB) można zapisać że
zadanie 2
wiedząc że wysokość w trójkącie równoramiennym dzieli podstawę na dwie równe część mogę zapisać
że AF=BF=5 , jest również dwusieczną kąta pomiędzy ramionami. Z twierdzenia o stycznych okręgu
otrzymujemy że AF=AD=5, zatem odcinek CD=8 bo AC=13. Licząc skalę podobieństwa trójkątów ABC i
CDE (trójkąty są podobne na zasadzie kkk, bo DE jest równoległe do AB) można zapisać że

 Zostały jeszcze dwa zadania
Zostały jeszcze dwa zadania 
 dobranoc wszystkim
dobranoc wszystkim


 ?
?





 nie ładnie obgadywać kogoś
nie ładnie obgadywać kogoś 
 "o wilku mowa"
"o wilku mowa" 


 Natomiast tutaj masz ładnie
napisane, czarno na białym
Natomiast tutaj masz ładnie
napisane, czarno na białym 




 moja siostra określiła to jako beżowy połączony z kawą i mlekiem
moja siostra określiła to jako beżowy połączony z kawą i mlekiem


 zaraz wrzucę skany moich obliczeń ale to
już w nowym poście
zaraz wrzucę skany moich obliczeń ale to
już w nowym poście



 Policz dobrze
Policz dobrze 

 bo za dwa lata o tej porze będziesz miał wolne
bo za dwa lata o tej porze będziesz miał wolne 


