liczby banan: Czy istnieje liczba dodatnia , której sześcian jest o jeden mniejszy od jej kwadratu ? mój typ na równanie to: t³−1=t² − dobrze?

konrad: t³=t²−1

Basia: dobrze tylko rozwiązać to równanie nie będzie łatwo (na poziomie szkolnym) bo nie ma pierwiastków wymiernych jeżeli ma być poziom szkolny spróbuj graficznie

Basia: oczywiście dobrze jest to co konrad napisał

banan: a możesz mi wytłumaczyć to równanie. Jak dla mnie szescian jest o jeden mniejszy od kwadratu, to t³−1=t²

konrad: no bo tak jest, ale Twoje równanie mówi odwrotnie

Basia: a jest o 1 mniejsze od 5 czyli a=5−1 = 4 zgadza się ? t³ jest o 1 mniejsze od t² ⇒ t³ = t²−1

picia: pytanie jest o liczby dodatnie http://www.wolframalpha.com/input/?i=x%5E3%3Dx%5E2-1

banan: ok juz czaje, a jak to narysować? sprawdzić wartości dla całkowitych t a potem narysować na oko?

Basia: t³ = t²−1 t³+1 = t² narysować: f(x) = t³+1 g(x) = t² będzie widać, że muszą się przeciąć, ale w punkcie o odciętej ujemnej czyli taka dodatnia nie istnieje

Basia: P.S. formalne rozwiązanie wymaga zastosowania pochodnych jeżeli znasz to mogę Ci napisać jak to zrobić jeżeli nie, to pisanie nie ma sensu

konrad: pochodnych? a nie tych skomplikowanych wzorów Cardano czy jakoś tak?

ICSP: pochodnych a wzory Cardano wcale nie są skomplikowane.

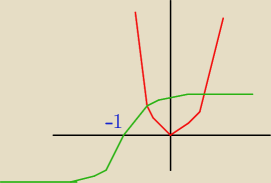
banan: one się przetną w dwóch miejscach

Basia: tu nie każą znaleźć tej liczby, a wykazać, że jedyne rozwiązanie równania t³ − t² + 1 = 0 jest ujemne łatwiej przy pomocy pochodnych gdyby kazali jej szukać to owszem tylko wzory Cardano

ICSP: t³ − t² = −1 t²(t−1) + 1 = 0 i tutaj mam że : t−1 < 0 ⇒ t < 1 − to jest według mnie oczywiste. Jednak dla t < 1 oraz t > 0 zarówno t² jak i (t−1) będą liczbami mniejszymi od 1. Iloczyn liczb mniejszych od 1 nigdy nie może dać liczby 1. Tak wiec nie istnieje liczba dodatnia spełniająca warunki zadania. c.n.u. Basiu może być dowodzik ?

Basia: @banan to zły rysunek wykres f(t) = t³+1 zupełnie inaczej wygląda poszukaj wykresu y = x³ i przesuń go o 1 w górę

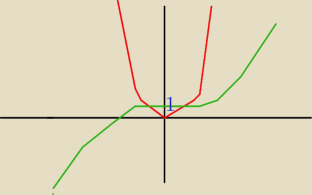
banan: tak?

Eta* :

Basia: @ICSP rozumiem ten dowód i jest w porządku, ale przydałoby się trochę jaśniej t=1 ⇒ 1−1 = −1 ⇒ 0= −1 fałsz t>1 ⇒ t³>t² ⇒ t³−t²>0 czyli nie może być równe −1 t∊(0,1) ⇒ 0<t²<1 i −1<t−1<0 ⇒ 0 < t² < 1 i 0 < −(t−1) < 1 ⇒ 0 < −t²(t−1) < 1 ⇒ t²(t−1) > −1 czyli nie może być równe −1 może być ?

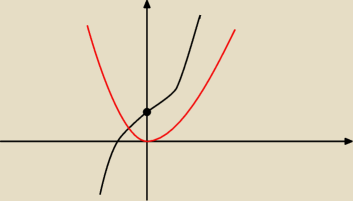
Basia: mniej więcej tak

ICSP: Basiu gratuluje zapisu dowodu. Ja bym na taki zapis nie wpadł

Mila: x³−x²+1=0 x²(x−1)+1=0 równanie może być spełnione dla x−1<0 ⇔x<1 rozważmy x∊(0,1) iloczyn |x²(x−1)|<1 x=0 nie jest pierwiastkiem równania w takim razie x<0

Mila: Oj, nie zauważyłam ICSP. dla ICSP

Mila: ICSP jeszcze Cię nie było, gdy pisałam.

Basia: a najprościej to chyba byłoby tak: t³ = t² −1 ⇔ t³+1 = t² czy to może zachodzić dla t∊(0;+∞) t =1 ⇒ 1³+1 = 1² ⇒ 2 = 1 sprzeczność t>1 ⇒ t³ > t² ⇒ t³+1 > t²+1 > t² ⇒ t³+1 i t² nie mogą być równe t∊(0,1) ⇒ t³>0 i t²<1 ⇒ t³+1>1 i t² < 1 ⇒ jak wyżej

Mila: Witaj Basiu.

Basia: Witaj Milu

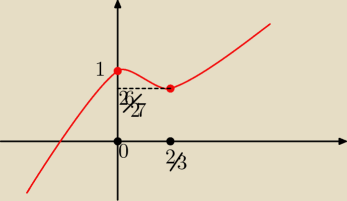
Basia: dla ciekawych jak to zrobić inaczej: t³ = t² − 1 t³ − t² + 1 = 0 i badamy przebieg zmienności f(t) = t³ − t² + 1 t∊R

	1		1
limt→−∞ (t3−t2+1) = limt→−∞ t3(1 −		+		) = −∞*(1−0+0) = −∞
	t		t3

	1		1
limt→+∞ (t3−t2+1) = limt→+∞ t3(1 −		+		) = +∞*(1−0+0) = +∞
	t		t3

f'(t) = 3t² − 2t = t(3t−2) f'(t) = 0 ⇔ t=0 ∨ t = ²₃ t∊(−∞;0) ⇒ f'(t)>0 ⇒ f(t) ↗ t∊(0;²₃) ⇒ f'(t)<0 ⇒ f(t)↘ t∊(²₃;+∞) ⇒ f'(t)>0 ⇒ f(t) ↗ stąd: t_max = 0 i f_max = f(0) = 1

	8		3
tmin = 23 i fmin = f(23) =		−		+ 1 =
	27		9

8−9+27		26
	=
27		27

i teraz można naszkicować wykres tej funkcji wygląda jak na rysunku wniosek: dla t∊(0;+∞) f(t)=t³−t²+1 nie ma miejsc zerowych ⇒ dla t∊(0;+∞) t³−t²+1≠0 dla t∊(0;+∞) t³≠ t²−1