Rozwiązać
miłosz: A=(2;∞), B=<−5;0>u(4;∞)
Mam podać A∪B, A∩B, A/B, B/A
Jak to wyznaczyć? Chodzi mi głównie o zbiór B
10 sie 14:53
Artur_z_miasta_Neptuna:
najlepiej narysuj sobie te przedziały na osi, a następnie:
A∪B −−−− to jest SUMA tych zbiorów
A∩B −−−− część wspólna (czyli tam gdzie zbiory się na siebie nakładają)
A/B −−− to co nalezy od zbioru A, ale nie należy do zbioru B (innymi słowy A/B = A/(A∩B))
B/A −−− analogicznie do tego wyższej
10 sie 14:58
10 sie 15:00
miłosz: Mógłbyś to szybko rozwiązać, bym zerknął, jak byś mógł
10 sie 15:00
Artur_z_miasta_Neptuna:
niee ... sam musisz to rozwiązać ... na spokojnie, bo inaczej będziesz się gubił, kiedy jest
zbiór domknięty, a kiedy nie (i dlaczego)
10 sie 15:11
Eta*:
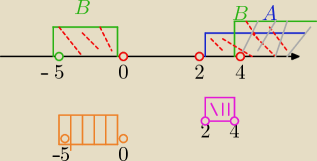
1/
A U B= <−5, 0) U (2,
∞)
2/
A∩B= .....
3/
A\B = ...
4/
B\ A=...
10 sie 15:13
miłosz: Dobra , ale sprawdź czy dobrze,
AuB=<−5,0>u(2,∞) AnB=(4,∞) A/B=(2,4) B/A=<−5,0)
10 sie 15:15
miłosz: Eta, dlaczego za zerem w AuB nawias jest nie jest domknięty?
10 sie 15:17
miłosz: chyba wiem, bo to suma całego zbioru i się zmienia na otwarty
10 sie 15:20
Artur_z_miasta_Neptuna:
Eta się pomyliła z tym domknięcie w 0 ... zarówno w 1) jak i w 4)
10 sie 15:21
miłosz: Ale czy moje jest dobrze (rozwiązanie)
10 sie 15:24
miłosz: ?
10 sie 15:24
Artur_z_miasta_Neptuna:
1) tak
2) tak
3) tak
4) domknij 0
10 sie 15:26
Artur_z_miasta_Neptuna:
3) też źle −−− domknąć 4.
10 sie 15:26
miłosz: Może właśnie powiedzieć , dlaczego tak nie otwarty?
10 sie 15:33
Artur_z_miasta_Neptuna:
A = (2,+
∞) czyli inaczej zapisując (2,4>∪(4,+
∞) ... prawda
B = (4,+
∞)
a więc: A/B = (2,4>
10 sie 15:37
Eta*:
Sorry
źle spojrzałam ,że B= <−5,0) U (4,
∞)
10 sie 15:37
Artur_z_miasta_Neptuna:
ach ten klon Ety
10 sie 15:40
miłosz: nadal nie rozumiem dlaczego w A/B jest tak (2,4> a nie tak (2;4) ,przecież tam gdzie 4 jest
nawias kółko niezamalowane
10 sie 16:04