Rozwiąż nierówności metodą algebraiczną i graficzną: Bajka: Rozwiąż nierówności metodą algebraiczną i graficzną: |3−|x+5||≤1 |3−|x−2||>2 |2−|x−3||≤0

Artur_z_miasta_Neptuna: 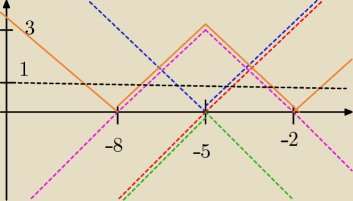czerwona to x+5 niebieska to |x+5| zielona to −|x+5| fiolet to 3−|x+5| pomarańcz −− to |3−|x+5||

Bajka: Czy można prosić o rozpisanie krok po kroku.

Artur_z_miasta_Neptuna: algebraicznie: |3−|x+5||≤1 ⇔ −1≤3−|x+5|≤1 ⇔ −1≤3−|x+5| ⋀ 3−|x+5|≤1 ⇔ |x+5|≤4 ⋀ 2≤|x+5| ⇔ ⇔ −4≤x+5≤4 ⋀ (−2≥x+5 ⋁ x+5≥2) ⇔ x≥−9 ⋀ x≤−1 ⋀ ( x≤−7 ⋁ x≥−3) ⇔ x∊<−9,−1>∩{(−∞,−7>∪<−3;+∞)} ⇔ x∊<−9,−7>∪<−3,−1> analogiczne pozostałe dwa przykłady

pigor: ...no to algebraicznie , łopatologicznie rzecz ujmując np. tak:: |3−|x+5||≤ 1 ⇔ −1≤ 3−|x+5|≤ 1 /+(−3) ⇔ −4≤ −|x+5|≤ −2 /*(−1) ⇔ ⇔ 4 ≥|x+5|≥2 ⇔ |x+5|≤ 4 ∧ |x+5| ≥2 ⇔ −4≤ x+5 ≤4 ∧ (x+5≤−2 ∨ x+5 ≥2) ⇔ ⇔ (−9≤ x ≤−1 ∧ x≤ −7) ∨ (−9≤ x ≤−1 ∧ x ≥−3) ⇔ −9≤ x ≤−7 ∨ −3≤ x ≤−1 ⇔ ⇔ x∊<−9;−7> U <−3;−1> − szukany zbiór rozwiązań, co widać na rys. powyżej

Artur_z_miasta_Neptuna: jest krok po kroku −−− idź kolorami od góry do dołu

Bajka: Napiszę swoje rozwiązanie jednego z przykładów czy mógłbyś je sprawdzić: |3−|x−2||>2 3−|x−2|>2 ∨ 3−|x−2|<−2 −|x−2|>−1 ∨ −|x−2|<−5 (czy w tym miejscu jak likwiduję znak minus przed wartością bezwzględną to zmieniam znak w nierówności na przeciwny, czy korzystam z jakiegoś twierdzenia wartości bezwzględnej) |x−2|>1 ∨ |x−2|<5 x−2>1 ∨ x−2<−1 ∨ x−2<5 ∧ x−2 >−5 x>3 ∨ x<1 ∨ x<7 ∧ x>−3 x∊ (−∞, −3) ∪ (1,3) ∪ (7, +∞)

Bajka: A jak rozwiązać taką nierówność algebraicznie: |2|x−1|−4|≥4

Artur_z_miasta_Neptuna: −|x−2| >−1 // mnożysz obustronnie przez (−1) |x+2| < 1

Artur_z_miasta_Neptuna: poza tym −−− zawsze możesz sprawdzić tutaj: http://www.wolframalpha.com/input/?i=%7C3-%7Cx-2%7C%7C%3E2

Bajka: Wielkie dzięki. Jeszcze tylko ta nierówność niżej, bo się gubię.

Artur_z_miasta_Neptuna: |2|x−1|−4|≥4 ⇔ −4≥2|x−1|−4 ⋁ 2|x−1|−4≥4 ⇔ −2≥|x−1|−4 ⋁ |x−1|−4≥2 ⇔ ⇔ 2≥|x−1| ⋁ |x−1|≥6 ⇔ .....

Artur_z_miasta_Neptuna: ojjj ... błąd |2|x−1|−4|≥4 ⇔ −4≥2|x−1|−4 ⋁ 2|x−1|−4≥4 ⇔ −2≥|x−1|−2 ⋁ |x−1|−2≥2 ⇔ ⇔ 0≥|x−1| ⋁ |x−1|≥4 ⇔ .....

pigor: ...i wychodzi x∊(−∞;−3>U{1}U<5;+∞) . ...

Bajka: A czy można to zrobić tak: |2|x−1|−4≥4 ||2x−2|−4≥4 |2x−2|−4≥4 ∨ |2x−2|−4≤−4 |2x−2|≥8 ∨ |2x−2|≤0 2x−2≥8 ⋁ 2x−2≤−8 ∨ 2x−2≤0 ⋀ 2x−2≥0 2x≥10 ⋁ 2x≤−6 ⋁ 2x≤2 ⋀ 2x≥2 x≤5 ⋁ x≤−3 ⋁ x≤1 ⋀ x≥1 x∊(−∞;−3>U{1}U<5;+∞)

Bajka: Mam jeszcze jeden przykład √x²+6x+9>5−|x|

picia: x²+6x+9=(x+3)²

Artur_z_miasta_Neptuna: jak widzisz ... mozna tak zrobić co do ostatniego przykladu −−− √(x+3)² = |x+3|

Eta: Równoważna nierówność |x+3|+|x|>5 rozpatrz przedziałami: 1/ x€ (−∞, −3) 2/ x€ <−3,0) 3/ x€<0,∞) jako odp: otrzymasz x€ ( −∞, −4) U (1,∞) powodzenia

picia: chcialem dac podpowiedz a nie cale rozwiazanie

Eta: Gdzie tu widzisz "całe rozwiązanie" ? picia

picia: no dobra, odpowiedz nie czytalem dokladnie Eta jestes dwa razy na forum...w spisie.

Eta: Pewnie ktoś się za mnie podszywa

Eta*:

Bajka: Czy to będzie tak: 1. x€ (−∞, −3) −x−3x>5 −2x>8 x<4 2. x€ <−3,0) x+3−x>5 0>2 sprzeczność 3. x€<0,∞) x+3+x>5 2x>2 x>1

Artur_z_miasta_Neptuna: czyli jakie będą ostateczne przedziały

Bajka: x∊(−∞,−4)∪(1,+∞)

Eta*:

Artur_z_miasta_Neptuna: Bajka −−− tak, dobrze (zrobiłaś/−eś parę literówek przy rozwiązywaniu, ale wyniki ostateczny jest dobrze)

Bajka: A mógłbyś je wskazać

Eta*: −x−3−x>5 ⇒ −2x > 8 ⇒ x < −4

Bajka: Dzięki.

Artur_z_miasta_Neptuna: tak jak klon Ety napisał brak '−' w 2 linijce brak '−' w 4 linijce