? Patryk:

	logmx
określ liczbę pierwiastków równania		=2 w zależności od wartości paramentu m
	log(x+3)

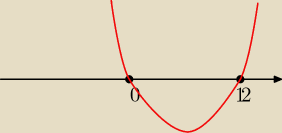
ja robie tak logmx=2log(x+3) logmx=log(x+3)² mx=x²+6x+9 x²+6x+9=mx x²+6x−mx+9=0 x²+x(6−m)+9=0 Δ=(6−m)²−36 =36−12m+m²−36= =m²−12m m(m−12) wiec 1 p dla 0 lub 12 0 p dla (0;12) 2 p dla (−∞;0)U(12;∞) odpowiedzi mam trochę inne czego zapomialem ?

Patryk: zad nr 2 dla jakich wartości parametru k równanie log₉27−log₃(x+√3)=k ma pierwiastek nalezący do przedziału (3√3;5√3) wyliczylem x

	√27−3k*√3
x=
	3k

	√27−3k*√3
3√3<		<5√3
	3k

czy to zadziala ?

Mila: Rozważ dziedzinę równania. Log(x+3)≠0 ⋀ x+3>0 ⋀ mx>0

picia: a dziedzina ?

Patryk: sprawdze

Patryk: log(x+3)≠0 x+3>0 mx>0 x≠−2 x>−3 nie wiem

pigor: ... a więc dalej : D_r : ponieważ mx>0 ⇔ (m>0 ∧ x>0) v (m<0 ∧ x<0) ⇒ x≠ −2 ∧ x>−3 ∧ mx>0 ⇔ ⇔ (x≠ −2 ∧ x>−3 ∧ m>0 ∧ x>0) v (x≠ −2 ∧ x>−3 ⋀ m<0 ∧ x<0) ⇔ ⇔ D_r={m, x : (m>0 ∧ x>0) ∨ (m<0 ∧ −3<x<−2) v (m<0 ∧ −2<x<0)}

Mila: zadanie 2.

	3
log927=
	2

3
	−k=log3(x+√3)⇔
2

3^3/2−k=x+√3 x=3^3/2−k−√3=3√3*3^−k−√3 3√3<3√3*3^−k−√3<5√3 /+√3 4√3<3√3*3^−k<6√3 /:√3 4<3*3^−k<6 /:3

4		1
	<(		)k<2 Dokończ
3		3

Patryk: dzięki