Zadania AS: Kto chce,niech liczy Zadanie 1 Wyznaczyć wzór iteracyjny, pozwalający obliczać kolejne przybliżenia dla ⁿ√A , A > 0 Zadanie 2 Wykazać,że funkcja x¹⁰⁰ + a*x + b ma nie więcej niż 2 miejsca zerowe. Zadanie 3 Czy równanie xⁿ + xⁿ⁻¹ + ... + x² + x − 1 = 0 ma pierwiastek dodatni. Jeżeli tak,to ile posiada pierwiastków dodatnich?

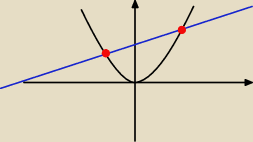
Trivial: Zadanie 2. Pierwiastków wielomianu poszukujemy rozwiązując równanie x¹⁰⁰ + ax + b = 0, czyli x¹⁰⁰ = −(ax+b). Dowód widoczny na rysunku.

Artur z miasta Neptuna: 2) d_f =R f` = 0 <=> x = a^1/99 Mozna dorzucic granice dla −/+∞ z powyzszych informacji wynika ze funkcja moze conajwyzej dwukrotnie przecinac os OX.

Vax: Ewentualnie jeżeli f(x) = x¹⁰⁰+ax+b, to widzimy, że f'(x) = 100x⁹⁹+a, skąd f'(x) = 0 ma dokładnie jedno rozwiązanie rzeczywiste, więc f(x) = 0 może mieć maksymalnie 2 rozwiązania rzeczywiste, cnd.

Vax: 3) f(x) = xⁿ+...+x²+x−1 ⇒ f'(x) = nxⁿ⁻¹ + ... + 2x+1, więc dla x>0 mamy f'(x) > 0, skąd dla x > 0 f(x) jest ściśle rosnąca, dodatkowo jest ciągła i f(0) < 0 , f(1) ≥ 0, stąd na mocy własności Darboux dostajemy, że f(x) ma w przedziale (0;1] jedno rozwiązanie, a skoro jest ściśle rosnąca dla x>0, więc jest to jedynie dodatnie rozwiązanie.

Artur z miasta Neptuna: Vax ... z darboux masz ze jest conajmniej jedno rozwiazanie (np. moga byc trzy) sprawe dokladnie iednego rozwiazanie zalatwia nam dopiero 'scisle rosnaca funkcja'

Tomek.Noah: nie wiem czy o to chodzi w pierwszym ale się podejme w sumie nie jest grzechem spróbować A∊R₊ ⁿ√A=x xⁿ=A xⁿ−A=0 f(x)=xⁿ−A f'(x)=n*xⁿ⁻¹

	xkn−A
xk+1=xk−
	nxn−1

	1		A
xk+1=xk−		xk−
	n		nxn−1

	(n−1)xkn−An
xk+1=
	nxkn−1

Było by tak?

Vax: Tak, to, że jest dokładnie jedno wynika właśnie z tego, że f jest ściśle rosnąca

Trivial: Tomek, nie może być tak, bo dla wartości x_k = ⁿ√A powinieneś dostać x_k+1 = ⁿ√A.