?
Patryk: Dla jakich wartości parametru m równanie x2−2x−log1/3m2=0 ma take dwa różne
pierwiastki,których suma kwadratów jest mniejsza od 6
1.
a2+b2<6
a2+2ab+b2−2ab<6
(a+b)2−2ab<6
4+4log1/3m<6
4+4log1/3m<6
2.Δ>0
4−4*(−log1/3m2)>0
4+8log1/3m>0
4+8log1/3m>0
czy do tego momentu nie mam błędu ?
7 sie 22:20
Artur z miasta Neptuna:
na razie dobrze
7 sie 22:30
Patryk: | | √3 | |
rozwiązuje te nierówności czerwona jak i niebieską i mam ( |
| ;√3) w odpowiedzaich jest |
| | 3 | |
| | √3 | | √3 | |
(−)√3;− |
| )U( |
| ;√3) napisać pełne rachunki ? |
| | 3 | | 3 | |
7 sie 22:36
Jack:
pewnie się walnąłeś opuszczając podstawy log − trzeba by zmienić znak nierówności. Pokaż
rachunki
7 sie 22:38
Patryk: chyba widzę błąd,ale nie do końca rozumiem, po drodze korzystam z wzoru logabc=clogab
i opuszczam kwadrat
7 sie 22:57
Eta:
Odpowiedzi w podręczniku są poprawne

7 sie 22:58
Patryk: juro się odezwę, idę spać
7 sie 23:00
pigor: ... no to może chcesz np. tak : z warunków zadania
m∊R\{0} , bo
m "siedzi" pod kwadratem pod logarytmem , zatem
x2−2x−log13m2=0 ⇔ x
2−2x+1=1+log
13m
2 ⇔
⇔ (x−1)
2=1+log
13m
2 , to stąd i z warunków zadania :
1+log
13m
2>0 i (x
1+x
2)
2−2x
1x
2<6 ⇔ log
13m
2>−1 i 4+2log
13m
2<6
⇔ m
2<3 i log
13m
2<1 ⇔ |m|<
√3 i m
2>
13 ⇔ |m|<
√3 i |m|>
1√3
⇔ −
√3<m<
√3 i (m<−
1√3 lub m>
1√3) ⇔
⇔
m∊(−√3;−1√3) U (
1√3;
√3) . ...

8 sie 00:04
Maslanek: Co te Viete'y tu robią?

8 sie 00:06
pigor: .. ano , w treści zadania jest mowa o sumie kwadratów 2−óch różnych pierwiastków,
czyli
x12+x22= x
12+2x
1x
2+x
22−2x
1x
2= (x
1+x
2)
2−2x
1x
2 .

8 sie 11:38
Maslanek: nie krzycz

Nie widziałem

8 sie 13:20
pigor: ... przepraszam , jeśli uznałeś to za krzyk ...

8 sie 13:36
Patryk:
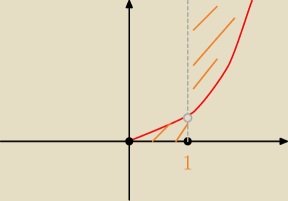
dzięki ,chyba rozumiem co skopałem, teraz mam takie zadane ,sprawdzicie ?
zaznacz na płaszczyźnie współrzędnych zbiór (x,y),których wsp spełniają nierówność
log
xy>2
D ,x>0 x≠1 ,y>0
y>x
2 dla x∊(1;
∞)
y<x
2 dla x∊(0;1)
8 sie 18:57
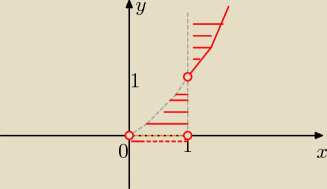
Eta:
Bez punktu (0,0)

8 sie 19:05
Patryk: dzięki
8 sie 19:07
Eta:

8 sie 19:07
Eta:
8 sie 19:16
Patryk:
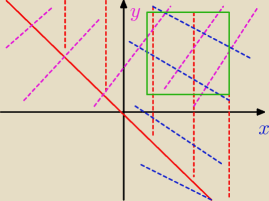
zaznacz na płaszczyźnie współrzędnych zbiór (x,y),których wsp spełniają równanie
log(x+y)=logx+logy
D x>0 y>0
x+y>0⇒y>−x
czy sama dziedzina jest ok ?
czyli dziedzina to tam gdzie ten zielony kwadrat czyli pierwsza ćwiartka układu wsp
to jets ok ?
8 sie 19:26
Patryk: ?
8 sie 20:11
Patryk: ?
8 sie 21:56
Aga1.: Dziedzina to pierwsza ćwiartka układu.
A skąd ten kwadrat?
8 sie 22:07
Eta:
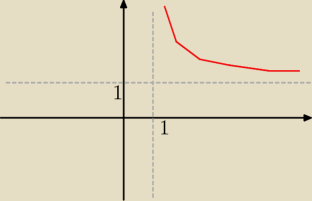
8 sie 22:10
Eta:
D: x>0 , y>0
log(x+y)= logxy
| | x | | 1 | |
x+y= xy ⇒ y= |
| = 1+ |
| |
| | x−1 | | x−1 | |
8 sie 22:14
Patryk: ok dzieki
9 sie 12:52
Patryk: ten kwadrat to miał oznaczać właśnie pierwsza cwiatke
9 sie 12:52
Patryk: zaznacz na płaszczyźnie współrzędnych zbiór (x,y),których wsp spełniają równanie
logxy(y−2x)=0
D y−2x>0 ⇒ y>2x
xy>0
xy≠1 dalej nie wiem co z dziedzina
9 sie 13:09
Patryk: ?
9 sie 16:08
Eta:
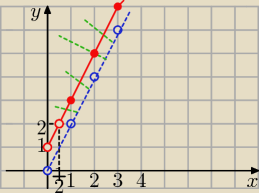
| | 1 | |
D: x>0 i y>0 i y>2x i xy≠1 ⇒ y≠ |
| |
| | x | |
log
xy(y−2x)=0 to: y−2x= 1 ⇒
y=2x +1 uwzględniając dziedzinę
| | 1 | | 1 | |
dla x= |
| to y= 2 A( |
| , 2) nie spełnia założeń , bo x*y =1 , a ma być ≠1 |
| | 2 | | 2 | |
B( 0,1) −− też odpada .........
Wykresem jest zbiór wszystkich punktów
czerwonej półprostej bez punktu A i bez B
9 sie 21:07
Mila: Piękne zadanko i pięknie rozwiązane.
9 sie 21:38
Mila: Patryk, a gdzie podziękowanie dla ETy?
9 sie 22:57
Eta:

A dla
Mili 
9 sie 23:02
Mila: Eto, zobacz "pewne" posty. Twój Achtung ( widać Poznanianka?) jakże uzasadniony.
Pozdrawiam.


9 sie 23:04
Patryk: dzięki Eta
10 sie 11:56
Eta:

10 sie 14:47




 Nie widziałem
Nie widziałem 

 dzięki ,chyba rozumiem co skopałem, teraz mam takie zadane ,sprawdzicie ?
zaznacz na płaszczyźnie współrzędnych zbiór (x,y),których wsp spełniają nierówność
logxy>2
D ,x>0 x≠1 ,y>0
y>x2 dla x∊(1;∞)
y<x2 dla x∊(0;1)
dzięki ,chyba rozumiem co skopałem, teraz mam takie zadane ,sprawdzicie ?
zaznacz na płaszczyźnie współrzędnych zbiór (x,y),których wsp spełniają nierówność
logxy>2
D ,x>0 x≠1 ,y>0
y>x2 dla x∊(1;∞)
y<x2 dla x∊(0;1)



 zaznacz na płaszczyźnie współrzędnych zbiór (x,y),których wsp spełniają równanie
log(x+y)=logx+logy
D x>0 y>0
x+y>0⇒y>−x
czy sama dziedzina jest ok ?
czyli dziedzina to tam gdzie ten zielony kwadrat czyli pierwsza ćwiartka układu wsp
to jets ok ?
zaznacz na płaszczyźnie współrzędnych zbiór (x,y),których wsp spełniają równanie
log(x+y)=logx+logy
D x>0 y>0
x+y>0⇒y>−x
czy sama dziedzina jest ok ?
czyli dziedzina to tam gdzie ten zielony kwadrat czyli pierwsza ćwiartka układu wsp
to jets ok ?


 A dla Mili
A dla Mili 


