mam problem z zadaniem :(( Madzia :): Pole trójkąta ostrokątnego ABC jest równe 100. Punkt D nalezy do boku AB i długość odcinka ADdo długosci odcina DB jest równy 7:3. Punkt E leży na boku AC i stosunek dł odcinka AE do dł odcinka AC jest równe 4:5 . oblicz pole S czworokąta DBCE. Z góry dziekuję

@Basia: Podpowiadam

@Basia:

AD
	= 73
DB

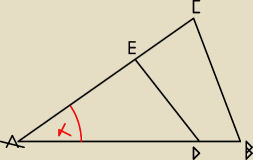
3*AD = 7*DB DB = ³₇*AD AB = AD+DB = AD+³₇AD = ¹⁰₇AD AD = ⁷₁₀AB = 0,7*AB

AE		4
	=
AC		5

5*AE = 4*AC AE = ⁴₅AC = 0,2*AC

	AB*AC*sinα
PABC =		= 100
	2

AB*AC*sinα = 200

	AD*AE*sinα		0,7*AB*0,2*AC*sinα
PADE =		=		=
	2		2

0,14*AB*AC*sinα		0,14*200
	=		= 14
2		2

P_DBCE = P_ABC − P_ADE = 100−14 = 86

Madzia :): Bardzo dziekuje

Mat: AE = 4/5AC = 0,2*AC hmm, ciekawe, a nie 0,8*AC? To zadanie z rozwiązaniem można znaleźć na przedostatniej stronie tego pdf'a