Okrąg opisany na stożku. Znajdz kąt rozwarcia BigMax: Stosunek pola powierzchni bocznej stożka do pola powierzchni kuli opisanej na tym stożku wynosi 3:8. Znajdź kąt rozwarcia tego stożka. Siedzę nad tym i siedzę i nie mogę. Proszę o pomoc

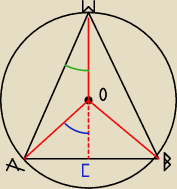
@Basia: kąt zieloiny α kat niebieski 2α R − promień kuli r − promień podstawy stożka b − tworząca stożka w △AWB sin2α = ^r_R r = R*sin2α = 2R*sinαcosα w △ACW sinα = ^r_b b = ^r_sinα = ^{2R*sinαcosα}_sinα = 2R*cosα

Pb
	= 38
Pk

πrb
	= 38
4πR2

rb
	= 32
R2

2R*sinαcosα*2R*cosα
	= 32
R2

4sinαcos²α=³₂ 8sinα(1−sin²α) = 3 −8sin³α + 8sinα − 3 = 0 8sin³α − 8sinα + 3 = 0 nie wiem czy to wystarczy bo tego równania nie umiem rozwiązać jeszcze pomyślę

@Basia: Jeszcze raz. Chyba teraz będzie dobrze

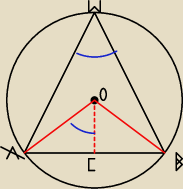
@Basia: kąty zaznaczone na niebiesko α z △ACO sinα = ^r_R r = Rsinα z △AWB i tw.cosinusów (2r)² = b²+b²−2b*b*cosα 4r² = 2b²(1−cosα) r² = ^{b2(1−cosα)}₂

	b√1−cosα
r =
	√2

	b√1−cosα
Rsinα=
	√2

	b√1−cosα
R =
	√2sinα

	b2(1−cosα)
R2 =
	2sin2α

πrb
	= 38
4πR2

rb
	= 32
R2

R*sinα*b
	= 32
R2

bsinα
	= 32
R

bsinα
	= 32
b√1−cosα   √2sinα

√2sin2α
	=32
√1−cosα

2√2*sin²α = 3√1−cosα 4*2*sin⁴α = 9(1−cosα) 8*sin²α*sin²α = 9(1−cosα) 8*(1−cos²α)² = 9(1−cosα) 8(1 − 2cos²α +cos⁴α) = 9 − 9cosα 8cos⁴α − 16cos²α + 9cosα −1 = 0 niestety to jest tak samo wredne (albo bardziej) jeżeli coś mi przyjdzie do głowy napiszę

@Basia: Proste jak budowa cepa. Teraz już się chyba nie pomyliłam.

@Basia: Guzik, jednak się pomyliłam

BigMax: W podpowiedziach pisze, żeby zastosować dwa razy twierdzenie sinusów.

@Basia: Też próbowałam. Cały czas dostaję to równanie 8sin³α − 8sinα + 3 = 0

@Basia: Też próbowałam. Cały czas dostaję to równanie 8sin³α − 8sinα + 3 = 0

pazio:

	1
no i co za problem? rozkładzasz wielomian. jednym z rozwiązań jest
	2

pazio: dostajesz U{1{2} i trójmian 4sin²α−2sinα+3=0 Δ jest niewymierna, tzn powstaje chyba (2√13)² i z tego chyba nie będzie rozwiązań

pazio: pomyłka: 4sin² + 2sinα − 3 = 0

Jacek Karaśkiewicz:

	−1 + √13
Dostajemy też niestety sinα1 =		i nie za bardzo wiadomo co dalej. Nie
	4

sprawdzałem poprawności równania, które rozwiązujemy, ale tutaj rzeczywiście ciężko coś z tym zrobić.

@Basia: Teraz wyszedł mi kompletny idiotyzm, a na dodatek nie widzę błędu. Napiszę to. Sprawdź

@Basia: Oznaczenia jak na pierwszym rysunku. ∡AWO=∡OAW = x ⇒ ∡AOW = 180−2x ∡AOC = x ∡AOB = 2x ∡CAO = 90−x z △AOW ^sinx_R = ^{sin(180−2x)}_b ^sinx_R = ^sin2x_b b = ^Rsin2x_sinx z △AOD sinx = ^r_R r = Rsinx r*b = R*sinx*^Rsin2x_sinx = R²*sin2x ^rb_4R² = ³₈ ^rb_R² = ³₂ ^R2*sin2x_R² = ³₂ sin2x = ³₂ a to jest niemożliwe bo sin2x∊<−1,1> wniosek: taka kula i stożek nie istnieją

@Basia: Napiszcie mi czy to jest dobrze ! Albo gdzie jest błąd

@Basia: To są dwa sprzeczne rozwiązania. Rzeczywiście równanie 8sin³x − 8sinx +3 = 0 ma jedno rozwiązanie sinx=¹₂ czyli x=30 czyli kąt rozwarcia = 60 drugim mogłoby być sinx = ^−1+√13₄ Gdzie do diabła jest błąd

@Basia: Błąd jest w pierwszym. Źle sobie kąt zapisałam. Niebieski ≠ 2x, niebieski = x

@Basia: Czyli poprawne rozwiązanie jest w poście z 11:22

@Basia: Nie, już mi się wszystko pokręciło. Jednak w pierwszym jest dobrze. W tym z 11:22 jest błąd. Tu są źle kąty oznaczone.

@Basia: Z tw.sinusów wychodzi to samo co w pierwszym. rb= ^R2*sin22x_sinx ^rb_R² = ^sin22x_sinx = ³₂ 2*2sinxcosx*sin2x = 3sinx 4cosx*2sinxcosx = 3 8sinxcos²x=3 8sinx(1−sin²x)=3 −8sin²x + 8sinx − 3 = 0 i nie ma inaczej no to sinx=¹₂ lub sinx=^−1+√13₄ czyli x=30 lub diabli wiedzą co czyli kat rozwarcia = 60 lub jak wyżej

pazio: a może trzeba tego drugiego sinusa przybliżyć do jakiegoś ułamka dziesiętnego i z tablic..?

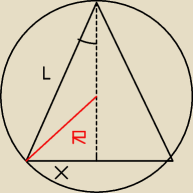
Jacek Karaśkiewicz: Trochę inaczej próbowałem to zrobić, mianowicie tak: Oznaczenia jak na rysunku, zaznaczony kąt to ^α₂.

	x		x
⑴ sin⍺2 =		⇒ L =
	L		sin⍺2

	3		πxL
⑵		=		⇒ 12R2 = 8xL
	8		4πR2

	2x		x
⑶		= 2R ⇒ R =
	sin⍺		sin⍺

Wstawiamy ⑴ i ⑶ do ⑵:

	x2		x
12 ⋅		= 8 ⋅ x ⋅
	sin2⍺		sin⍺2

12		8
	=
sin2⍺		sin⍺2

8sin²⍺ = 12sin^⍺₂ 16sin^2⍺₂cos^2⍺₂ = 12sin^⍺₂ 4sin^2⍺₂(1 − sin^2⍺₂) = 3sin^⍺₂ ... 4sin^4⍺₂ − 4sin^2⍺₂ + 3sin^⍺₂ = 0 Jedyny pierwiastek z przedziału [−1, 1] to sin^⍺₂ = 0.

@Basia: niby można, ale to już przecież nie jest dokładne rozwiązanie 3,6<√13<3,7 ale bliżej mu do 3,6 czyli sinx≈0,65 i odczytać z tablic innej możliwości nie ma

@Basia: @Jacek Nie mam teraz już czasu, ale tu jest błąd 8sin²⍺ = 12sin^⍺₂ 16sin^2⍺₂cos^2⍺₂ = 12sin⍺ bo sin²α = (2sin^α₂cos^α₂)² = 4sin^2α₂cos^2α₂ czyli 32 nie 16 dalej będzie to co poprzednio

Jacek Karaśkiewicz: Racja Basiu. Powinno być rzeczywiście: 32sin^2⍺₂cos^2⍺₂ = 12sin^⍺₂ 8sin^2α₂(1 − sin^2α₂) = 3sin^α₂ ... 8sin^4⍺₂ − 8sin^2⍺₂ + 3sin^⍺₂ = 0 No i faktycznie wychodzą dwa pierwiastki z zakresu [−1, 1] i ten problem z √13.

@Basia: No cóż zasadniczo przyjmuje się, że wyznaczenie f.trygonometrycznych (sinusa i cosinusa) jest równoznaczne z wyznaczeniem kąta.

	−1+√13
sinα=
	4

	13−2√13+1		16 − 14 + 2√13		2(1+√13)
cos2α=1 −		=		=
	16		16		16

	√2(1+√13)
cosα=
	4

koszmarne, ale wyznaczone

@Basia: Chyba coś z tego jeszcze można zrobić. Interesuje nas właściwie kąt 2α

	√13−1		√2(1+√13)
sin2α = 2sinαcosα = 2*		*		=
	4		4

2		1		√2*12		√24
	*√2(√13−1)(√13+1) =		*√2(13−1) =		=		=
16		8		8		8

√4*6		2√6		√6
	=		=
8		8		4

cos²2α = 1−⁶₁₆=¹⁰₁₆

	√10
cos2α=
	4

to już trochę lepiej wygląda

michal2377: Otrzymujemy równanie 8sinα³−8sinα+3=0 podstawiamy pomocniczą t: sinα=t 8t³−8t+3=0 z twierdzenia o wymiernych pierwiastkach wielomianu o współczynnikach całkowitych otrzymujemy że jednym z pierwiastków jest ¹₂ czyli ten wielomian wygląda tak : W(t)=(t−0,5)(8t²+4t−6) obliczamy pierwiastki tego równania kwadratowego tj. t=^−1+√13₄ lub t=^−1−√13₄ (nie spełnia warunków zadania ponieważ w przybliżeniu ta liczba wynosi ok −1,15 a dziedziną sinusa jest <−1;1>) czyli mamy dwa pierwiastki t= ¹₂ lub t = ^−1+√13₄ (przybliżamy tą liczbę, ok 0,6514) czyli sinα = ¹₂ lub sinα = ^−1+√13₄ ok 0,651 Wyszukujemy kąt w tablicach trygonometrycznych tj ok 40,5 stopnia α=30st lub α=40,5 Kąt rozwarcia stożka wynosi 60 st. lub 81 st. ponieważ szukane nasze to sin2α

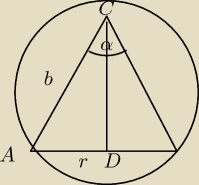
Krl: Michał wynik dobry. A może mi ktoś powiedzieć co ja mam źle? Z treści zadania

	3R2
rb=
	2

Z tw. sinusów:

2r
	=4R
sinα

Z f−nkcji tryg dla ΔADC:

	α		r
sin		=
	2		b

Rozwiązując ten układ wychodzą mi złe wyniki.] Ktoś mi wytłumaczy dlaczego?

Mila: Wyszedł mi kąt rozwarcia 90⁰.?

Mila: Rozważam teraz II przypadek.

Krl:

	α		α
Mi z tego wychodzi, że sin		= 0 co jest niemożliwe albo 16cos		−3=0
	2		2

Mila: Napiszcie wynik, bo chcę uniknąć błedów rachunkowych.

Krl: Wynik jest taki jak ma michał2377 (60 i 81) st

Mila: Napiszę po 21.

Mila: Mam identyczne równanie jak Michał. Krl źle zastosowałeś tw. sinusów tam ma być 2R. Pozdrawiam.