"matematyka.pisz pomysł na zadanie każdego dnia"
Saizou :
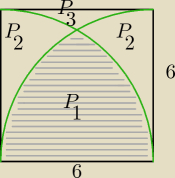
Oblicz pole zacieniowanego fragmentu
7 sie 11:23
konrad: no i?
7 sie 11:29
Saizou : 
myślę jak to zrobić
7 sie 11:31
konrad: to myśl, bo ja też nie wiem
7 sie 11:33
pigor: no to ja napiszę jak do tego doszedłem, ale
bez opisu (reszta jest ... milczeniem) ,a więc
np. tak :
P1 = 12*
π3*6
2 + (
12*
π3*6
2−
14+6
2√3) =
=
π3*36−
14*36
√3 = 12π−9
√3 =
3(4π−3√3) . ...
7 sie 11:35
konrad: dobra ja już wiem, przydało się zapisanie tego jako układu równań
7 sie 11:35
konrad: ale wyszedł mi zły wynik
7 sie 11:39
pigor: .. ja co do swego wyniku wcale nie jestem pewien na 100 %, tak, że spokojnie panowie . ...
7 sie 11:41
7 sie 11:46
konrad: ja znalazłem w swoich obliczeniach błąd ale teraz mi wyszło nieskonczenie wiele rozwiązań
7 sie 11:46
pigor: ...
aha! no to fajnie
rumpek , a chłopcy niech popracują . ...
7 sie 11:56
Mila: Saizou, narysuj linie pomocnicze (cięciwy), aby powstał Δ równoboczny.
7 sie 12:09
Saizou :
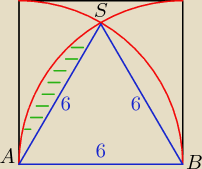
| | 36√3 | |
trójkąt ABS jest trójkątem równobocznym zatem jego pole wynosi |
| =9√3
|
| | 4 | |
zacieniowany fragment ma pole równe
P
z=P
wyć 60o−P
t
P
Z=6π−9
√3
zatem pole szukane to
2P
z+P
t=12π−18
√3+
√3=12π−9
√3
7 sie 12:11
Saizou : Mila właśnie na to wpadłem, ale rysunek nie chciał mi się wczytać
7 sie 12:12
konrad: co to jest P
wyc 60 i Pt
7 sie 12:13
konrad: dobra, Pt już wiem
7 sie 12:13
Saizou : Pwyć60o− pole wycinka koła o mierze 6o
Pt− pole trójkąta równobocznego
7 sie 12:14
Saizou : Pwyć60−pole wycinka koła o mierze kąta 60o
7 sie 12:15
konrad: okej, to rozumiem wszystko poza tym dlaczego jest π*60 a nie π*36 ?
7 sie 12:18
Saizou : błąd przy przepisywaniu
7 sie 12:18
konrad: aha
7 sie 12:20
Mila: Rysunek − piękny ( jak Ty to robisz?)
Masz tam błąd w jednym zapisie Pz ( pewnie literówka przy przepisywaniu, bo dalej jest dobrze)
Ładne rozwiązanie, wiem, że "wpadłeś" na pomysł (po czasie można się zorientować).
7 sie 12:22
Saizou : co do rysunku to:
narysowałem sobie kwadrat z gotowych figur, następnie użyłem opcji rysowanie łuków (ostatnia w
pierwszym rzędzie), dale użyłem linii prostej aby narysować ramiona trójkąta
7 sie 12:26
Mila: Dzięki Saizou, chodziło mi o te łuki.
7 sie 12:36
Saizou : nie ma za co
7 sie 12:37
Saizou : to może jeszcze jedno zadanko z cyklu "matematyka.pisz pomysł na zadanie każdego dnia"
7 sie 12:38
Mila: Dla Saizou i dla Kejt
Z dwóch stacji wyjeżdżają jednocześnie naprzeciw siebie dwa pociągi. Pierwszy jedzie z
prędkością 15 km/h większą niż drugi. Pociągi spotkały się po 40 minutach jazdy. Gdyby drugi
pociąg wyjechał o 9 minut wcześniej od pierwszego, to pociągi spotkałyby się w połowie drogi.
Obliczyć odległość między stacjami.
7 sie 12:46
Mila: Zadanie 2
Po zelektryfikowaniu linii kolejowej prędkość średnia pociągu osobowego wzrasta o 10 km/h, zaś
czas jazdy na trasie 200km zmniejsza się o 1 godzinę. W ciągu ilu godzin przejedzie pociąg
osobowy trasę 200 km po zelektryfikowaniu linii?
7 sie 12:52
Saizou : | | 8 | |
odpowiedź do pierwszego to 108 |
| km |
| | 9 | |
7 sie 13:34
Mila: 1) 90km. szukaj błędu.
2) 4h
7 sie 13:56
Saizou : a do drugiego 5h
7 sie 13:58
Saizou : w drugim 4 bo zapomniałem odjąć jedynki
7 sie 13:58
Maslanek: Mila
Powiedz mi jaki błąd popełniam. Bo już głupieje
x
1(t)=(V+15)t
x
2(t)=x−Vt
1 spotkanie: x
1(40)=x
2(40) ⇒ 40(V+15)=x−40V
2 spotkanie: x
1(31)=x
2(40) ⇒ 31(v+15)=x−40V
| | x | |
Albo nawet jeśli 2 spotkanie jest źle, to weźmy takie równanie: x1(31)= |
| ⇒ 62(v+15)=x. |
| | 2 | |
W każdym razie w obu przypadkach wychodzą pierdoły...
7 sie 14:41
Mila: | | 40 | | 2 | |
40minut= |
| h= |
| h jednostka czasu to godzina. |
| | 60 | | 3 | |
Jeśli Ci nie wyjdzie to więcej podpowiem.
7 sie 15:36
Maslanek: Chciałem w minutach, bo nie ma problemu z 31minutami
7 sie 15:43
Maslanek: Głupoty dalej.
V= −15
x= −10
7 sie 15:51
Maslanek: Dobra... jakoś lipnie rozwiazany ten układ
7 sie 15:54
Maslanek: | | 4 | |
Tak to i tak lipnie w drugim przpyadku, bo wychodzi V=15, x=34 |
| . |
| | 9 | |
Czemu? −,−
7 sie 15:55
Saizou : | | 8 | |
nie wiem czemu się tak zrobiło ale tam miało być że x+y=108 |
| km |
| | 9 | |
7 sie 20:11
rumpek: co to kurka jest
?
7 sie 20:14
Saizou : tez chciałbym wiedzieć
rumpek
7 sie 20:15
rumpek: widzisz, ułamkami popsułeś strukturę forum
pewnie musiałeś dać U{ } { } w układzie równań,
dobrze mówię
?
7 sie 20:18
Saizou : właśnie nie bo układ był liniowy
7 sie 20:19
Saizou : mógłby ktoś ten post usunąć, napiszę jeszcze raz rozwiązanie
7 sie 20:21
Saizou : ale to mogło być spowodowane tym że po układzie dałem ułamki
7 sie 20:22
Eta:
7 sie 20:23
Saizou : Eta normalizuje forum
7 sie 20:26
7 sie 20:29
Eta:
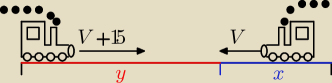
Ładny rysunek
tzn.
lokomotywy
7 sie 20:31
rumpek: ciekawsze byłby "tupolewki"
7 sie 20:32
Saizou :
| | 2 | |
I po 40 minutach czyli po |
| h
|
| | 3 | |
− dla pociągu T
−dla pociągu S
2V+15=3y 2V=3x
3x+10=3y
II gdy pociąg S wyjechał 9 minut wcześniej
− dla pociągu T
−dla pociągu S
2940=27x+27y
Obliczając układ równań:
3x+10=3y
2940=27x+27y
mam nadzieję że chochlików nie ma
7 sie 20:33
Saizou : jeszcze zapomniałem że ten po prawej to francuski TGV, a ten po prawej to japoński
Shinkansen
7 sie 20:35
Saizou : że ten po lewej to TGV
7 sie 20:35
Saizou : Mila widzę że w samą porę odwiedziłaś forum
7 sie 20:39
Eta:
Po 40 min
s= x+y
| | 2 | | 2 | | 2 | |
s= |
| (v+15)+ |
| v ⇒ s= |
| (2v+15) |
| | 3 | | 3 | | 3 | |
| | s | | 9 | | v | |
gdyby ...... to: |
| = t*(v+15)= (t+ |
| )*v ⇒ t= |
| |
| | 2 | | 60 | | 100 | |
s= 2t(v+15)
| | 2 | | v | |
|
| (v+15)= 2* |
| *(v+15) |
| | 3 | | 100 | |
dokończ..............
7 sie 20:40
Saizou : Eto przynajmniej coś ładnego
7 sie 20:40
Mila: 1) wskazówka :
v− prędkość szybszego pociągu
v−15 prędkość wolniejszego pociągu
| | 2 | |
− obliczyć przebytą drogę dla każdego pociągu w ciągu |
| h |
| | 3 | |
−obliczyć całą drogę,
−obliczyć połowe drogi,
| | 9 | |
−obliczyć drogę przebytą w ciągu |
| h |
| | 60 | |
t −czas , w którym obydwa pociągi jechały.
No to panowie do dzieła. (rachunki są brzydkie, wyniki ładne)
7 sie 20:40
Eta:
Poprawka zapisu w ostatniej linijce
| | 2 | | v | |
|
| (2v+15) = 2* |
| (v+15) |
| | 3 | | 100 | |
7 sie 20:44
Mila: Saizou, gdy już się doliczysz sposobem Ety albo (lub) moim, to mogę dać nowe zadanie− prędkość,
droga czas. Chcesz łatwe, czy trudne?
7 sie 20:45
7 sie 20:47
Saizou : a dlaczego Eto?
7 sie 20:49
Saizou : Mila na dziś prędkości mi wystarczy, w końcu żyjemy w świecie małych prędkości, jak to mój
fizyk mawia
7 sie 20:50
Saizou : V1=60
zatem x=40
V2=75
zatem y=50
s=50+40=90 km
7 sie 20:52
Saizou : czyli jakbym liczył moim sposobem z dodatkową zmienną "t" oznaczającą czas to zadanie dałoby
się rozwiązać?
7 sie 20:54
Mila: Saizou drugi pociąg jechał dłużej o 9 minut, aby przebyć połowę drogi. Czas wspólnego
podróżowania dałeś 40 minut, a to nie jest prawdą. U mnie i u Ety jest inaczej.
Przeanalizuj dokładnie ten przykład.
7 sie 21:01
Mila: No to szkoda, że się poddajesz, na maturze prawie, zawsze jest zadanie tego typu, no troche
łatwiejsze.
7 sie 21:02
Saizou : dobrze wiedzieć
i się nie poddaje tylko prędkość mi już bokiem wychodzi na fizyce przy
teoriach Einsteina
7 sie 21:08
Mila: Nagroda dla Saizou
Znaleźć długość dwusiecznej kąta prostego w trójkącie prostokatnym o przyprostokątnych a i b.
7 sie 21:17
Saizou :
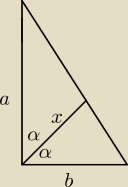
α=45
| ab | | 1 | | 1 | |
| = |
| *a*x*sin45+ |
| *b*x*sin45
|
| 2 | | 2 | | 2 | |
| ab | | ax | | √2 | | bx | | √2 | |
| = |
| * |
| + |
| * |
|
|
| 2 | | 2 | | 2 | | 2 | | 2 | |
2ab=x(a
√2+b
√2)
7 sie 21:25
Mila:
Pięknie.
Wyłącz √2 z mianownika i usun niewymierność.
7 sie 21:39
7 sie 21:42
Mila:
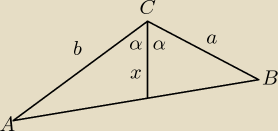
W trójkącie ABC dane są dwa boki a i b oraz kąt C=120
0.Znaleźć długość dwusiecznej kąta C.
7 sie 21:48
Saizou :
| ab | | ax | | bx | |
| *sin120= |
| *sin60+ |
| sin60
|
| 2 | | 2 | | 2 | |
| ab | | √3 | | ax | | √3 | | bx | | √3 | |
| * |
| = |
| * |
| + |
| * |
|
|
| 2 | | 2 | | 2 | | 2 | | 2 | | 2 | |
ab
√3=ax
√3+bx
√3
7 sie 22:01
Mila: Bardzo dobrze.
7 sie 22:03
Saizou : tylko trochę to zadanie jest nieprecyzyjne bo na dobrą sprawę jeden z boków mógł być długością
AB
7 sie 22:05
Eta:
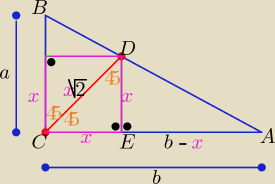
Inny sposób
|CD|=x
√2
Z podobieństwa trójkątów AED i ABC
7 sie 22:06
Mila:
7 sie 22:14
Eta:
Zad1/ Dane są trzy liczby dodatnie a,b,c takie,że
| | a | |
Wyznacz wartość ilorazu |
| |
| | b | |
7 sie 22:16
Saizou : to może teraz trochę trudniejsze zadanie
7 sie 22:16
Eta:
Proszę bardzo
7 sie 22:17
Saizou : już się boję, jak Eto nad twoimi w miarę prostymi zadaniami można siedzieć godzinami
7 sie 22:19
Eta:
7 sie 22:20
Saizou :
a
2−ac=b
2
ac=ab+b
2
a
2−ab−b
2=b
2
a
2−b
2−ab−b
2=0
(a−b)(a+b)−b(a+b)=0
(a+b)(a−b−b)=0
(a+b)(a−2b)=0
| | a | |
a+b=0→a=−b sprzeczność bo a,b∊D lub a−2b=0→a=2b→ |
| =2 |
| | b | |
7 sie 22:39
Mila: wykaż, że prawdziwa jest równość:
3√20+14√2+3√20−14√2=4
7 sie 22:43
Saizou : 3√(2+√2)2+2√(2−√3)3=2+√3+2−√3=4 cnw
7 sie 22:49
Saizou : tam zamiast 2 przy pierwiastkach mają być 3 i to samo w potęgach
7 sie 22:49
Saizou : napiszę to jeszcze raz bo widzę same błędy
3√(2+√2)3+3√(2−√2)3=2+√2+2−√2=4
7 sie 22:54
Mila: Podnieś do 3 potęgi (2+√2)− rozpisz szczegółowo.
7 sie 22:55
Eta:
7 sie 22:56
Saizou : (2+√2)3=23+3*22*√2+3*2*(√2)2+(√2)3=8+12√2+12+2√2=20+14√2
7 sie 23:02
konrad: odwrotnie
7 sie 23:06
Saizou : to
konrad przeczytaj od lewej
7 sie 23:07
Saizou : *do prawej
7 sie 23:07
konrad: sorry
7 sie 23:12
Mila: Dobrze jest, myślałam, że odpisałeś odpowiedź, bo coś szybko było.
7 sie 23:14
nikt : Saizou mam dla ciebie zadanie
Rozwiąż równanie :
(2
√2 + 1)x
3 + 6x
2 + 3
√2x + 1 = 0
7 sie 23:18
Saizou : Mila tu zastosowałem taki trick który nie zawsze działa, ale dla małych liczb się
sprawdza
zawsze można pomyśleć na podstawie wzoru (a+b)
3=a
3+3a
2b+3ab
2+b
3, przy założeniu że "b" to
będzie pierwiastek
3a
2b+b
2=14
√3
a
3+3ab
3=20
7 sie 23:18
Maslanek: Błędów
7 sie 23:19
nikt : wracam za 20 min i chce widzieć rozwiązanie
7 sie 23:21
Saizou : może będzie
7 sie 23:21
Eta:
100 moja
7 sie 23:25
Maslanek: 101 moje
7 sie 23:26
Saizou : to ja będę miał
101 dalmatyńczyków
7 sie 23:26
Eta:
To mój
jamnik
7 sie 23:28
Maslanek: Ja biorę furę
7 sie 23:28
Eta:
7 sie 23:28
Saizou : 
jak japońscy turyści w Polsce
7 sie 23:31
Saizou : nikt czy ty nie masz co robić w domy tylko mi życie komplikujesz
7 sie 23:38
nikt : oj tam od razu komplikuje
Pozwalam ci się nacieszyć fajnym wielomianem
P.S. Sam go ułożyłem. Specjalnie dla ciebie
7 sie 23:44
Saizou : mogę się założyć że to coś ciężkiego
7 sie 23:46
nikt :
7 sie 23:48
Maslanek: Końcówka:
[x(√2+1)+1][x2(3−√2)+x(2√2−1)+1]=0.
Zgadza się?
7 sie 23:50
Maslanek: W sumie proste. Polega na grupowaniu wyrazów. Wpadasz na pomysł i rozwiązane.
7 sie 23:50
Maslanek: Dodam, że nie sprawdzałem tylko leciałem na gorąco, ale wyszło coś normalnego, więc zakładam,
ze całkiem nieźle
7 sie 23:51
nikt : Maslanek grrr
To było dla
Saizou
7 sie 23:53
Maslanek: Przecież rozwiązania nie ma
Tylko delikatna podpowiedź
Najpeirw próbowałem usunąć niewymierności, ale to się nie
trzymało kupy
7 sie 23:55
Saizou : ja dzisiaj już nie myślę nikt jutro postaram się coś wykombinować
7 sie 23:56
nikt : Delikatna podpowiedź to to nie jest xD
Ja z takiej podpowiedzi mogę już bez problemu odczytać jak to pogrupować
Myślę że
Saizou też
Zaraz mu wymyśle jeszcze kilka takich równanek
7 sie 23:57
Mila: Dobranoc wszystkim
)
7 sie 23:58
Saizou : nikt nie kłopocz się na dzisiaj już koniec z zadaniami
7 sie 23:58
Saizou : Dobranoc Mila, miłych snów
7 sie 23:58
Maslanek: Czy ja wiem...
Ja myślałem nad pogrupowaniem dobre 3 minuty. 2 nieudane próby
A potem już zwątpiłem póki
nie ujrzałem światła
8 sie 00:00
Saizou : no nic ja idę spać i mówię wam wszystkim Dobrej nocy
8 sie 00:34
Mila:
Prezent dla Saizou.
Dwa samochody wyruszyły jednocześnie naprzeciw siebie z miast odległych o 210 km i jadą ze
stałymi prędkościami. W chwili mijania jeden z nich ma jeszcze 2 godziny jazdy, zaś drugi
| | 9 | |
|
| godziny jazdy do miasta z którego jedzie samochód mijany. Obliczyć prędkość każdego |
| | 8 | |
samochodu.
8 sie 15:44
Saizou : v
1 prędkość pierwszego samochodu
v
2− prędkość drugiego auta
t− całkowity czas potrzebny do przejechania 210 km
| | 210 | | 210 | | 210 | |
v1= |
| →t= |
| , a do miejsca spotkania to: |
| −2
|
| | t | | v1 | | v1 | |
analogicznie dla v
2
| | 210 | | 210 | | 9 | |
zatem można zapisać |
| −2= |
| − |
|
|
| | v1 | | v2 | | 8 | |
podobnie robię z drogami pozostałymi do przebycia
s
1=2v
1
wówczas mam układ równań
Obliczając ten układ wychodzi że
v
1=60 v
2=80 lub v
1=420 v
2=−560 druga para odpada bo prędkość nie może być ujemna
zatem pozostaje
v1=60kmh v2=80kmh
8 sie 19:40
Mila: Bardzo dobrze.
Zrobiłam nieco inaczej,może trochę krócej, wrócimy do zadania przed maturą.
8 sie 20:37
