Rozwiąż nierówność z modułem jacek: Rozwiąż nierówność 3 ≤ I x I < 9

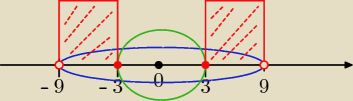
Artur_z_miasta_Neptuna: możliwość 1. (tradycyjna) 3≤|x| <9 ⇔ dla x≥0: 3≤x<9 ⋀ dla x<0: −3≥x>−9 x∊(−9;−3> ∪ <3;9) możliwość 2. (graficznie) −−− patrz rysunek niebieski przedział − zielony przedział możliwość 3. 3≤|x| <9 ⇒ |x|<9 ⋀ |x| ≥3 ⇒ x∊(−9,9) ⋀ x ∉ (−3,3)

jacek: Dzięki !

jacek: powinno być zbiór pusty, dlatego , że jest iloraz a nie suma

Basia: to nie jest zbiór pusty

jacek: nie rozumiem proszę o wyjaśnienie

pigor: ... rozwiązanie analityczne może wyglądać np. tak : 3≤|x|<9 ⇔ (x≤ −3 ∨ x≥3) ∧ −9<x<9 ⇔ (x≤ −3 ∧ −9<x<9) ∨ (x≥3 ∧ −9<x<9) ⇔ ⇔ −9< x ≤ −3 ∨ 3≤ x 9 ⇔ x∊(−9;−3> U <3;9) . ...

jacek: a jeżeli równanie byłoby takie 3≥IxI>9 to co ?

pigor: ... to np. tak : 3≥IxI>9 ⇔ −3≤x≤3 ∧ (x<−9 ∨ x>9) ⇔ (−3≤x≤3 ∧ x<−9) ∨ (−3≤x≤3 ∧ x>9) ⇔ ⇔ x∊∅ ∨ x∊∅ ⇔ x∊∅ . ...

ICSP: 3 ≥ |x| > 9 ⇒ 3 > 9 − mamy sprzeczność.