Zadanai AS: Kto chce,niech liczy. Zadanie 1 W sześciokącie foremnym różnica między mniejszą przekątną a bokiem sześciokąta wynosi m. Oblicz różnicę między najdłuższą i najmniejszą przekątną tego sześiokąta. Zadanie 2 Na trzech półprostych wychodzących z punktu A i parami prostopadłych odmierzono odcinki AM = AN = a, AP = 2*a.Znaleźć odległość punktu A od płaszczyzny MNP. Zadanie 3 Dowieść,że 3 ! ! ! ma więcej niż 1000 cyfr.

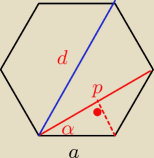
Aga1.: p−a=m d−p=? d=2a α=30⁰ p=a√3 a√3−a=m a(√3−1)=m

	m		m(√3+1)
a=		=
	√3−1		2

Trivial: Zadanie 3. Korzystając z https://matematykaszkolna.pl/forum/151757.html mamy n! ≥ n^n/2 ((3!)!)! = (6!)! = 720! ≥ 720³⁶⁰ ≥ 700³⁶⁰ = 7³⁶⁰*10⁷²⁰. Teraz wystarczy pokazać, że 7³⁶⁰ > 10²⁸⁰. Załóżmy, że to prawda i weźmy obustronnie logarytm dziesiętny. 360log7 > 280

	280		7
log7 >		=		= 0.777777...
	360		9

Teraz bierzemy kalkulator albo tablicę logarytmów i sprawdzamy ile wynosi log7. log7 ≈ 0.845. Zatem OK.

AS: Podaję moje rozwiązanie zadania 3 3! ! ! = 720! = 1*2*3*...*720 > 101*102*...*720 > 100*100*...* 100 (620x) = 100⁶²⁰ = 10¹²⁴⁰ > 10¹⁰⁰⁰

Trivial: AS, nawet tak nie próbowałem, a powinienem był.

pigor: 2) np. tak : niech x=? , a z warunków zadania długości PM=PN=a√3 i MN=a√2 i P_ΔMNP=¹₂a√2√3a²−¹₂a²=¹₂a²√5 ,więc ¹₃x* P_ΔMNP= ¹₃*¹₂a²*2a ⇒ x* ¹₂a²√5= a³ ⇔ ⇔ x= ²_√5a , czyli x=0,4√5a − szukana odległość A od pł. ΔMNP . ...

AS: Mój wynik w zadaniu 2: x = 2*a/3

pigor: no jasne liczyłem " w pamięci" i nie wziąłem do kwadratu , bo powinno być PM=PN=a√5 ⇒ P_ΔMNP= ³₂a² i x*³₂a²= a³ ⇔ x=²₃a ,. ...