Rzut równoległy ''': Rzutem równoległym odcinka AB na prostą m w kierunku prostej k jest odcinek A'B'. Wówczas: a.) Jeśli |A'B'| = |AB| to AB ∥ m b.) może się zdarzyć że |A'B'| = |AB| i prosta k tworzy z prostą m kąt o mierze 41 stopni c.) Jeśli prosta k jest prostopadła do prostej m to |AB| ≥ |A'B'| Wg odpowiedzi poprawna jest odpowiedź "b" i "c". Dlaczego "a" nie?

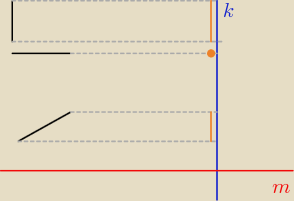
Artur_z_miasta_Neptuna: rysunek przedstawia wersję dla m⊥k jeden z odcinków AB jest tak ustawiony, że |AB| || m ... jak widzisz ... rzut tego odcinak na 'k' jest punktem (co przeczy odpowiedzi a) stąd widać, że odpowiedź 'c' prawidłowa

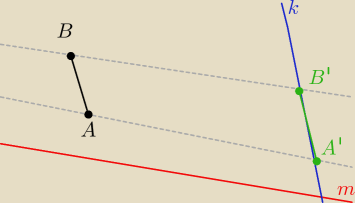
Artur_z_miasta_Neptuna: odpowiedź (b) jest podchwytliwa ... otóż ... bez różnicy jaki kąt jest pomiędzy k i m (pod warunkiem, ze nie są one równoległe −−− czyli kąt = 0^o) jeżeli |AB| || k ... to rzut równoległy do prostej m na prostą k będzie takiej samej długości rysunek trochę koślawy ... ale nie czepiać się (szare przerywane || m .... |AB| || k ... |A'B'| pokrywa się z 'k')

Artur_z_miasta_Neptuna: tak więc ... odpowiedź (b) jest prawidłowa ... bo 'może się zdarzyć', że |AB| || k ∧∡(k,m) = 41^o

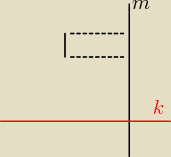
''': Ale to miał być rzut równoległy na prostą m w kierunku prostej k. Jeśli chodzi o b, to chyba niczego to nie zmienia, ale w a wychodzi mi ciągle coś takiego jak na rysunku...

Artur_z_miasta_Neptuna: treść wskazuje na rzut na prosta k gdzie rzut jest równoległy wzgledem prostej m

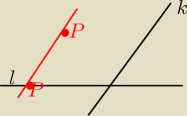
''': To ja już niczego nie rozumiem. W podręczniku jest definicja " rzutem równoległym na prostą l w kierunku prostej k nazywamy takie przekształcenie geometryczne, które każdemu punktowi P płaszczyzny przyporządkowuje taki punkt P' prostej l, że przez punkty P i P' można poprowadzić prostą równoległą do k" i do tego jest rysunek( ten punkt P leżący niżej jest punktem P', nie wiem dlaczego, ale nie mogłam napisać tam ')

cloud: mój post jest spóźniony .. w każdym razie, ''' ma rację. na pierwszy rzut oka wydaje się, iż to zadanie można zinterpretować dwojako, aczkolwiek na początku mamy wyraźnie napisane: na prostą m, czyli wszystkie rzutowane figury będą "trafiały" na prostą m. ktoś mógłby przyczepić się o "prostą m w kierunku prostej k", jednak wcześniejsze "AB na prostą m" daje nam do zrozumienia, że chodziło o "prostą m w kierunku WYZNACZONYM PRZEZ prostą k".