dowód
Saizou :
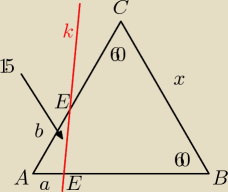
Korzystając z rysunku i własności podanych na nim, wykaż, że a + b = x, czyli:
|BC| = |AC| = |AB| = |AE| + |AD|
5 sie 12:19
rumpek: pomyliłeś oznaczenia, dałeś dwa razy E
5 sie 12:19
Saizou : tam przy kącie 15
o ma być D
5 sie 12:20
Saizou : jakaś podpowiedź?
5 sie 12:24
rumpek: Wypisz sobie wzory na pola trójkąta
5 sie 12:27
rumpek: 
. Zapomniałem podać najważniejsze dane, mianowicie: Stosunek pól jest równa 1:5
5 sie 12:29
Saizou : P=
√p(p−a)(p−b)(p−c)
5 sie 12:31
5 sie 12:33
rumpek: tak
5 sie 12:35
5 sie 12:35
rumpek: jak tamte wzory wypisałeś to lecisz, już widać coś
5 sie 12:38
Saizou : | | 1 | | 1 | | √3 | | ab√3 | |
PADE= |
| *ab*sin60= |
| *ab* |
| = |
|
|
| | 2 | | 2 | | 2 | | 4 | |
| | a2√3 | | ab√3 | | a√3(a−b) | |
PBCDE= |
| − |
| = |
|
|
| | 4 | | 4 | | 4 | |
a
√3(a−b)=5b*a
√3
a−b=5b
a=6b
5 sie 12:44
Jack:
"a" zdaje się że dwa razy co innego oznacza.
5 sie 12:49
rumpek: postaraj wyznaczyć się a i b
5 sie 12:49
rumpek: własnie powinno być we wzorze:
5 sie 12:49
Saizou : x2=6ab
x=√6ab
5 sie 13:01
rumpek: pokaż cały dowód a nie elementami
5 sie 13:07
Saizou : | | 5abc√3 | | ab√3 | | 6ab√3 | |
PABC= |
| + |
| = |
|
|
| | 4 | | 4 | | 4 | |
x
2√3=6ab
√3
x
2=6ab
x=
√6ab
a teraz idę na obiad
5 sie 13:15
rumpek: no i co to niby jest
to nie dowód
5 sie 13:27
Saizou : nie mam nic pomysłów
5 sie 13:32
rumpek: pomęcz jeszcze
, jak na nic nie wpadniesz koło 15 postaram się rozwiązać
5 sie 13:33
Saizou : to może tak:
załóżmy, że teza jest prawdziwa, zatem
a+b=x
korzystając z tego co wyliczyłem , że
x2=6ab
mogę zapisać że
(a+b)2=6ab
a2+b2=4ab
(a−b)2=2ab co jest spełnione tylko dla a=0 lub/i b =0
co jest sprzecznością bo boki trójkąta muszą być dodatnie, zatem a+b=x
cnd
wiem że są to kompletne bzdury ale i tak nic nie wymyślę
5 sie 14:38
Jack:
trochę mija się z celem zakładanie prawdziwości tezy. Poza tym, ostatnią równość można
rozwiązać traktując a (lub b) jako zmienną...
rumpek niech zapisze rozwiązanie
5 sie 15:00
rumpek:
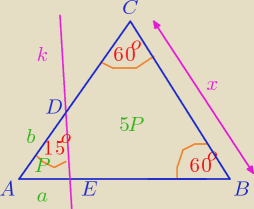
T:
a + b = x
1
o △AED(15
o, 60
o, 105
o)
b * sin15
o = a * sin105
o
(*) = sin15
o = sin(45
o − 30
o) = sin45
o*cos30
o − cos45
o*sin30
o =
| | √2 | | √3 | | √2 | | 1 | | √6 | | √2 | | √6 − √2 | |
= |
| * |
| − |
| * |
| = |
| − |
| = |
| |
| | 2 | | 2 | | 2 | | 2 | | 4 | | 4 | | 4 | |
(**) = sin105
o = sin(60
o + 45
o) = sin60
o * cos45
o + cos60
o * sin45
o =
| | √3 | | √2 | | 1 | | √2 | | √6 | | √2 | | √6 + √2 | |
= |
| * |
| + |
| * |
| = |
| + |
| = |
| |
| | 2 | | 2 | | 2 | | 2 | | 4 | | 4 | | 4 | |
| | √6 − √2 | | √6 + √2 | |
b * |
| = a * |
| / * 4 |
| | 4 | | 4 | |
b * (
√6 −
√2) = a * (
√6 +
√2)
| | a(√6 + √2) | | √6 + √2 | | a(√6 + √2)2 | |
b = |
| * |
| = |
| = |
| | √6 − √2 | | √6 + √2 | | 6 − 2 | |
| | a(6 + 2√12 + 2 | | a(8 + 4√6) | |
= |
| = |
| = (2 + √6)a |
| | 4 | | 4 | |
| | x2√3 | | x2√3 | |
2o 6P = |
| ⇒ P = |
| |
| | 4 | | 24 | |
Dalej tak jak napisał
Jack Wyraź jako zmienne i otrzymasz rozwiązanie
Oczywiście
przelicz wszystko bo może być gdzieś chochlik.
Tymczasem uciekam, jakby były problemy
dokończę po 18.
5 sie 15:02
Saizou : moja trygonometria do takiego poziomu to jeszcze nie doszła
5 sie 15:07
rumpek: Mówiłem, że będzie chochlik
Poprawka:
| | a(6 + 2√12 + 2) | | a(8 + 4√3) | |
(*) = |
| = |
| = (2 + √3)a |
| | 4 | | 4 | |
5 sie 15:13
Jack:
1o powinno być b=(2+√3)a (pomyłka w ostatnim wierszu tego punktu przy zamianie pierwiastka)
5 sie 15:15
rumpek:
5 sie 15:20
Maslanek: To to samo co b=a tg15?
5 sie 16:55
Saizou : Eto można prosić jakieś zadanko
5 sie 18:35
Eta:
Zad1/ dane są odcinki
a i
b
skonstruuj odcinki
x i
y takie,że x+y= a i by= ax
Zad.2/ Wyznacz wszystkie liczby całkowite , dla których
| | (9x2−4)(x+1) | |
liczba: |
| jest całkowita |
| | 3x3+2x2−3x−2 | |
| | 1 | |
Zad.3/ Wyznacz trzydziestą cyfrę po przecinku liczby |
| |
| | 7 | |
5 sie 18:45
Saizou : może zacznę od zadania 2
to sobie rozpisze
(9x
2−4)(x+1)=(3x−2)(3x+2)(x+1)
3x
3+2x
2−3x−2=3x
3−3x+2x
2−2=3x(x
2−1)+2(x
2−1)=(x
2−1)(3x+2)=(x−1)(x+1)(3x+2)
| (9x2−4)(x+1) | | (3x−2)(3x+2)(x+1) | | 3x−2 | |
| = |
| = |
|
|
| 3x3+2x2−3x−2 | | (x−1)(x+1)(3x+2) | | x−1 | |
wyznaczając dziedzinę
x∊R\{1}→x∊C\{1}
5 sie 19:09
rumpek: przepraszam, ale że to jest Twoja odpowiedź? poprawna to x∊{0,2}
5 sie 19:14
Eta:
| | 3*5−2 | | 13 | |
Np; dla x= 5 |
| = |
| ∉C |
| | 5−1 | | 4 | |
5 sie 19:15
konrad: ja tu nie jestem specem, ale chyba to nie koniec tego zadania
5 sie 19:15
rumpek: | | 3x − 2 | | 3(x − 1) + 1 | | 1 | |
(*) = |
| = |
| = |
| + 3[Snickers i jedziesz dalej ] |
| | x − 1 | | x − 1 | | x − 1 | |
5 sie 19:15
Eta:
rumpek ...... zepsułeś zabawę ! zad. było przeznaczone dla
Saizou
5 sie 19:17
rumpek: ale przecież nie rozwiązałem go
5 sie 19:18
Eta:
Zadania przeznaczone tylko dla Saizou !
5 sie 19:18
rumpek: przy zadaniach nie ma takiej informacji
Ale przecież nie rozwiązałem
5 sie 19:20
Eta:
i <
snikers >
5 sie 19:20
Saizou : teraz to proste:
| | 1 | |
trzeba znaleźć taki x, żeby |
| było całkowite zatem x∊{0 ; 2} |
| | x−1 | |
5 sie 19:20
rumpek: ale napisz, jak to znalazłeś
5 sie 19:21
Eta:
Odpowiedz ładnie .......
rumpkowi
5 sie 19:22
Saizou : zadanie 3
| 1 | |
| =0,(142857)→ że 30 liczba po przecinku to 7 |
| 7 | |
5 sie 19:23
Saizou : 1 żeby dało liczbę całkowitą musi być dzielone przez −1, albo 1
zatem mogę zapisać że
x−1=−1 albo x−1=1
x=0 albo x=2
5 sie 19:25
Eta:
A sto trzydziesta piąta ?
5 sie 19:25
Saizou : 2
5 sie 19:27
Eta:
Zad.4/ W trapezie długość dłuższej podstawy jest równa k
Pozostałe trzy boki trapezu są równe.
Proste będące przedłużeniami ramion przecinają się w punkcie P pod kątem 2α.
Wyznacz obwód trapezu.
5 sie 19:32
Eta:
5 sie 19:32
Saizou : ale jaszcze zostało zadanie konstrukcyjne, a konstrukcji to ja nie lubię
5 sie 19:33
Eta:
Zad.1/ koniecznie ! ( nie ma : "nie lubię"
5 sie 19:35
Eta:
Zad.1/ jest
5 sie 19:36
rumpek: to ja może nie ruszam
5 sie 19:38
Eta:
@
rumpek zad1. pozwalam
5 sie 19:46
Saizou : mogę zapisać że
odmierzając ile razy b mieści się w a mogę stwierdzić, że tak samo musi być w odcinkach x i y
| | b | | 1 | | y | | 1 | |
zatem mogę stwierdzić że stosunek |
| = |
| , zatem stosunek |
| = |
| .
|
| | a | | 4 | | x | | 4 | |
dzieląc odcinek a na 5 równych części mogę stwierdzić że jedna część to y, a 4 części to x
5 sie 19:52
Saizou :
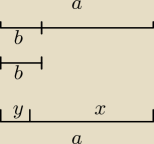
+ rysunek
5 sie 19:58
Eta:
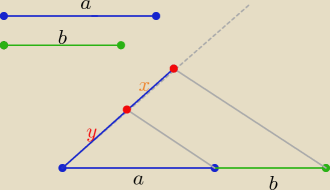
5 sie 22:09
rumpek: robisz to zadanie 4
? bo jest najlepsze ze wszystkich
5 sie 23:29
Eta:
5 sie 23:36
Saizou :
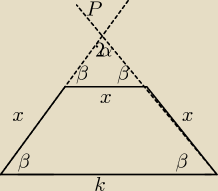
β=90−α
Ob
trapezu=3x+k
jakaś podpowiedź
5 sie 23:39
rumpek:
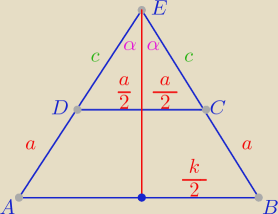
Proszę
5 sie 23:44
Saizou : czyli mam wyliczyć k w zależności od a i c
a(a+c)=ck
6 sie 00:09
rumpek: 
, skoro masz podane k ....
6 sie 00:10
6 sie 00:15
rumpek: podać rozwiązanie
?
6 sie 00:21
Saizou : nie, bo cię jeszcze
Eta dopadnie i wszystko będzie na mnie
6 sie 00:22
rumpek: ok
6 sie 00:22
Saizou : no nic ja mówię dobranoc wszystkim, a jutro może mnie oświeci
dobranoc
6 sie 00:34
rumpek: 
6 sie 00:37
rumpek: a zadanko czeka
6 sie 16:43
Saizou : rumpek cały czas myślę nad tym zadaniem
6 sie 17:37
rumpek:
6 sie 17:38
konrad: w tym zadaniu chodzi o to żeby podać obwód trapezu w zależności od α i k?
6 sie 17:52
rumpek: 
ale nie podawaj wyniku, bo to zadanie dla
Saizou
6 sie 18:01
konrad: wyniku to ja jeszcze nie wiem
ale myślę
6 sie 18:03
6 sie 18:09
rumpek: oj chyba nie
pokaż obliczenia powiem gdzie bład jest
6 sie 18:17
konrad: wyszed łmi taki sam wynik co Saizou
6 sie 18:22
Saizou : α=x dla wygody pisania
| | | | k | | k | |
sinx= |
| →sinx= |
| →(a+c)2sinx=k →a+c= |
|
|
| | a+c | | 2(a+c) | | 2sinx | |
| | | | a | | a | |
sinx= |
| →sinx= |
| →c2sinx=a→c= |
|
|
| | c | | 2c | | 2sinx | |
| a*2sinx+a | | k | |
| = |
|
|
| 2sinx | | 2sinx | |
| a(2sinx+1) | | k | |
| = |
|
|
| 2sinx | | 2sinx | |
a(2sinx+1)=k
| | 3k | | 3k | | k*2sinx+k | | 4k+k*2sinx | |
Ob= |
| +k= |
| + |
| = |
| |
| | 2sinx+1 | | 2sinx+1 | | 2sinx+1 | | 2sinx+1 | |
6 sie 18:26
rumpek: | | 3 | |
jest ok, tylko forma lepsza to: k( |
| ) |
| | 2sinα + 1 | |
6 sie 18:36
konrad: | | 3k | |
ale przecież to nie to samo co: |
| +k ? |
| | 2sinx+1 | |
6 sie 18:41
rumpek: | | 3 | |
tak zapomniałem jedyneczki napisac czyli : k( |
| + 1) |
| | 2sinα + 1 | |
6 sie 18:46
Saizou : to może jeszcze jakieś zadanko, tylko nie geometria
6 sie 18:49
Eta:
6 sie 19:04
Saizou : witaj Eto
6 sie 19:06
Eta:
6 sie 19:07
Saizou : to co może zadanko
tylko
NIE geometria
6 sie 19:08
Eta:
Za chwilę
..... a czemu nie geometria ?
6 sie 19:09
Saizou : na obecną chwilę mam jej dosyć
6 sie 19:11
rumpek: geometria jest najlepsza
6 sie 19:14
Eta:
Zadania dla Saizou !
zad.1/ Wyznacz wszystkie całkowite wartości parametru "m", tak aby pierwiastkiem
równania x3+mx2−75=0 była liczba pierwsza.
zad.2/ Dla jakiej wartości parametru "m" równanie : x3+mx2+2099x−2009=0
spełniają trzy różne liczby naturalne? Wyznacz te liczby.
6 sie 19:16
rumpek:
P.S. coś czuję, że
Saizou odechce się też algebry
6 sie 19:18
rumpek: 1 zrobione
w zasadzie w pamięci
6 sie 19:20
Eta:
6 sie 19:22
Saizou : Eto moje zdolności wielomianowe mówią mi, że nie potrafią tego zrobić, choć myślą że
takich wartości parametrów jest nieskończenie wiele
6 sie 19:29
rumpek: myśli Cię oszukują
6 sie 19:33
Eta:
6 sie 19:38
Saizou : to przerasta moje możliwości
6 sie 19:43
Eta:
Podpowiedź: wzory Viete
'a dla równania stopnia trzeciego ........ i jedziesz
6 sie 19:44
rumpek:
n(n − 1) = 20
ile wynosi n?
[nie można liczyć Δ]
6 sie 19:44
Eta:
n=5
6 sie 19:44
rumpek:
6 sie 19:46
Saizou : to wzory Viete'a istnieją również dla wyższych wielomianów?
6 sie 19:50
rumpek: no pewnie
, dla tutaj wzór nie trzeba
6 sie 19:52
rumpek: przynajmniej dla 1/
6 sie 19:52
6 sie 19:52
Eta:
Do zad.1/ niekoniecznie
ale ......... można
6 sie 19:54
Saizou : to nie na moją głowę zadanie
6 sie 20:00
Saizou : to już wolę geometrię
6 sie 20:00
rumpek: Can I ?
6 sie 20:01
Eta:
Następne zadania dla Saizou
Zad.3/ Uzasadnij,że dla każdej liczby całkowitej n
liczba M= (n−2)(n−1)n(n+1)+1 jest kwadratem liczby całkowitej
zad.4/ Uzasadnij,że liczba 3√10+6√3+3√10−6√3 jest całkowita
6 sie 20:02
rumpek: mówiłem, że algebry też się odechce
[
19:18 ]
6 sie 20:02
Saizou : here you are
6 sie 20:02
Eta:
Zobacz wpis
rumpka z
19: 18
6 sie 20:03
rumpek: "Can I" było do
Ety Aby nie było jak wczoraj xD
6 sie 20:03
Eta:
Echh
6 sie 20:04
rumpek:
6 sie 20:05
rumpek:
1/
x
3+mx
2−75=0 [to teraz zastosuje to co mówiłem abyś rozwiązał z n]
x
2(x + m) − 75 = 0
x
2(x + m) = 75
x
2(x + m) = 5 * 5 * 3
x
2(x + m) = 5
2 * 3
x + m = 3
5 + m = 3
m = −2
6 sie 20:07
konrad: 4 zadanie jest chyba najłatwiejsze
6 sie 20:08
rumpek: + komentarz dla bezpieczeństwa: rozpatrzono tylko dodatnie z samej definicji liczy pierwszej
6 sie 20:08
Eta:
No to na rozgrzewkę dla (nieco załamanego )
Saizou 
zad.5/ (łatwe)
Wiedząc,że |y+3| ≤5 oraz |x−1|≤3
Wyznacz największą i najmniejszą wartość iloczynu
x*y
6 sie 20:11
Eta:
Zad.1/ ze wzorów Viete
'a
| | −d | |
x1*x2*x3= |
| = 75 = 3*5*5 , bo x1 x2, x3 −−−są liczbami pierwszymi |
| | a | |
teraz W(3)= 27+9m−75= 0 ⇒ m∉ C −− odpada
W(5)= 125+25m−75=0 ⇒ m= −2 € C
odp: m= −2
6 sie 20:16
Saizou : y∊<−8;2>, a x∊<−2:4>
zatem yxmax= −8*(−2)=16
yxmin=−8*4=−32
6 sie 20:17
6 sie 20:19
rumpek: no i bierzemy się za lepsze zadania
6 sie 20:21
Saizou : tam żeby wykazać że jest to liczba całkowita to trzeba to co jest pod pierwiastkiem "ściągnąć"
do wzorów na (a±b)3?
6 sie 20:23
Eta:
Dokładnie
6 sie 20:24
pigor: w 1) może przesada korzystać z wzorów Viete'a , ale w 2). warto . ...
bo pierwiastki całkowite (o ile istnieją) "siedzą" wśród podzielników wyrazu wolnego, tu
75=3*25=3*5*5 i dalej jak wyżej . ...
6 sie 20:29
rumpek: pigor a niby jak ja zrobiłem
?
6 sie 20:30
Saizou : 3√(1+√3)3+3√(1−√3)3=1+√3+1−√3=2 ∊C
6 sie 20:30
Eta:
A czemu niby czemu "przesada"
( jak kto chce tak liczy
6 sie 20:36
pigor: ... a do zad.
2) Dla jakiej wartości parametru "m" równanie : x3+mx2+2099x−2009=0 spełniają
trzy różne liczby naturalne? Wyznacz te liczby. odp.
1,41,49 . ...
6 sie 20:36
Eta:
Zad.2/
A m= ? ..........
6 sie 20:37
rumpek: Eta złapała pigora
6 sie 20:42
Eta:
Raczej "wigora"
6 sie 20:43
rumpek: gra w skojarzenia
6 sie 20:49
Eta:
6 sie 20:50
Eta:
Gdzie jest
Saizou ?
6 sie 20:52
rumpek: całkuje
6 sie 20:53
Saizou : w lesie
tak myślę nad tym zadaniem i stwierdzam że trzeba to jakoś pogrupować, żeby były
tylko kwadratami liczb
n
4−3n
3−n
2+2n+1
6 sie 20:55
rumpek: zgadza się "
Jasiu"
6 sie 20:59
Saizou : przed chwilą zdobyliśmy brąz w zapasach i mamy szanse na medal w podnoszeniu ciężarów
6 sie 20:59
Saizou : Jasiu
nie mam na imię Jasiu, choć tak myślę że to może tyczyć się przysłowia
6 sie 21:01
rumpek: M= (n−2)(n−1)n(n+1)+1 = (n
2 − 1)(n
2 − 2n) + 1 = n
4 − 2n
3 − n
2 + 2n + 1 = ...
miałeś
error
6 sie 21:02
rumpek: dlatego było w ""
6 sie 21:02
Eta:
Błąd w mnożeniu!
6 sie 21:04
Saizou : chochlik przy przepisywaniu z mojego kajeciku
6 sie 21:05
Eta:
Ok
wybaczam
No to dokończ zadanie
6 sie 21:06
nikt : to zadanie z (n−2)(n−1)n(n+1) + 1
Chyba się nie powstrzymam xD
6 sie 21:07
Eta:
6 sie 21:07
Eta:
Oglądam
6 sie 21:08
rumpek: (*) = n
4 − 2n
3 + n
2 − 2n
2 + 2n + 1 = (ciekawe czy będzie lanie od
Ety )
6 sie 21:09
Saizou : mam szanse na medal
6 sie 21:10
nikt : Eta ale ja znam taką fajną metodę rozwiązania tego xD
Tzn pogrupowania tego wielomianu stopnia IV XD
6 sie 21:10
pigor: ...
liczby te to podzielniki naturalne wyrazu wolnego 2009 i 1+41+49= −m ⇒
m= −91
.
6 sie 21:10
Saizou : z/w
6 sie 21:10
Eta:
Wiem,że znasz
ale poczekajmy na
Saizou
Na razie czekam na medal
6 sie 21:13
Saizou : (n
2−n−1)
2
6 sie 21:38
nikt :
a teraz pisz całe rozwiązanie
6 sie 21:38
rumpek: dla
Saizou − nowa waluta
[niedługo zamieni euro]
6 sie 21:39
Saizou : dłuuuugo by pisać nikt
6 sie 21:42
nikt : pisz
6 sie 21:43
Saizou : ale jak nalegasz to poczekaj chwilę
6 sie 21:43
Eta:
6 sie 21:45
rumpek: jak długo
napisałem ci odpowiedź w moim poście
o
21:09
(*) = n
4 − 2n
3 + n
2 − 2n
2 + 2n + 1 = (n
2 − n)
2 − 2(n
2 − n) + 1 = (n
2 − n − 1)
2
6 sie 21:46
nikt : rumpek nudy xD
mając wielomian :
n4 − 2n3 − n2 + 2n + 1 postaramy się rozwiązać równanie :
n4 − 2n3 − n2 + 2n + 1 = 0
n4 − 2n3 = n2 − 2n − 1
n4 − 2n3 +n2 = 2n2 − 2n − 1
(n2−n)2 = 2n2 − 2n − 1
(n2 − n + a)2 = 2n2 − 2n − 1 + 2n2a − 2na + a2
(n2 − n + a)2 = (2+2a)n2 −(2+2a)n + a2 − 1
na oko widać że wyrażenie po prawej stronie możemy zawinąć do wzoru skróconego mnożenia dla a =
−1
mamy zatem :
(n2 − n − 1)2 = 0n2 − 0n + 1 − 1
(n2 − n − 1)2 = 0
stąd wniosek :
n4 − 2n3 − n2 + 2n + 1 = (n2 − n − 1)
6 sie 21:48
rumpek: moje rozwiązanie jedna linijka
6 sie 21:49
rumpek: ISCP chcesz zadanie ze stereometrii
?
6 sie 21:49
nikt : a moje wygląda ładniej
6 sie 21:49
rumpek: wątpię
6 sie 21:50
nikt : rumpku mam swoje z trygonometrii
Jednak mogę spróbować zrobić twoje
6 sie 21:50
konrad: rumpka rozwiązanie jest bardzie zrozumiałe
6 sie 21:51
Eta:
dla
rumpek za "jedną linijkę"
6 sie 21:53
nikt : Nie potraficie docenić prawdziwej sztuki
6 sie 21:53
Saizou : to może teraz jakiś dowód nie geometryczny
6 sie 21:53
6 sie 21:54
Eta:
Zad. 10 Czy liczba 77777777777777777777777777777777777
jest kwadratem liczby naturalnej ?
Uzasadnij odp
6 sie 21:54
Saizou : Eta ile jest tych siódemek
6 sie 21:57
Eta:
Tyle co napisałam
6 sie 21:58
Saizou : 36?
6 sie 21:59
rumpek:
Zadanie dla
ISCP aka.
nikt
Mając ostrosłup prawidłowy czworokątny ściana boczna nachylona jest do płaszczyzny podstawy pod
kątem α. Z krawędzi podstawy a poprowadzono płaszczyznę tworzącą z płaszczyzną podstawy kąt β.
Z: 0 < β < α. Oblicz P otrzymanego przekroju.
W sumie zadanie bardzo proste tylko liczenia trochę
6 sie 22:00
Eta:
6 sie 22:00
rumpek: Saizou 666
6 sie 22:00
nikt : rumpek ty tak specjalnie czy przez przypadek ?
6 sie 22:00
Saizou : tych siódemek jest jednak 35
6 sie 22:00
Eta:
6 sie 22:01
rumpek: nikt w sensie, którego postu
?
6 sie 22:01
Saizou : rumpek oblicz sumę 36 wyrazów ciągu arytmetycznego o różnicy 1
6 sie 22:02
Eta:
Ja pytałam , czy ta liczba jest kwadratem liczby naturalnej!
A nie............. ile jest w niej
siódemek
6 sie 22:02
rumpek:
6 sie 22:03
Eta:
6 sie 22:04
Saizou : nie bo żadna liczba naturalna podniesiona do kwadratu nie da liczby składającej się z
jednakowych cyfr, z wyjątkiem 1
6 sie 22:04
nikt : w sensie "ISCP"
6 sie 22:04
6 sie 22:05
rumpek:
6 sie 22:05
rumpek: czemu nick zmieniłeś
tamten był jak "kozak" z lasu
6 sie 22:06
rumpek: aaa "ICSP"
6 sie 22:06
nikt : owiedz mi czy ten przekrój będzie trapezerm równoramiennym o wysokości
6 sie 22:08
nikt : Nick zmieniłem ponieważ według mnie ten bardziej oddaje mój poziom
6 sie 22:08
Eta:
6 sie 22:09
Eta:
Moje
200 
6 sie 22:09
Saizou : nikt to ja powinienem mieć "minus nieskończoność wiedzy matematycznej"
6 sie 22:10
nikt : oj
Saizou uwierz mi
Jesteś dużo lepszy ode mnie
6 sie 22:11
Eta:
6 sie 22:12
rumpek: nikt po co ci ta 2 tam
? i zacznij wpierw od rysunku
6 sie 22:12
Saizou : nikt nie wierzę Tobie
6 sie 22:12
Saizou : masz na pocieszenie
6 sie 22:13
rumpek: lepsze jabłko
lub karnet na "pakernie"
6 sie 22:13
Maslanek: Wolałbym dobrą furę
6 sie 22:14
nikt :
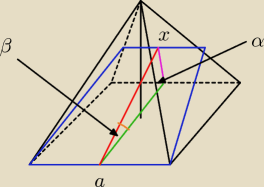
z twierdzenia sinusów mam że
| | asinα | |
h = |
| = czerwony |
| | sin(α+β) | |
teraz pytanie :
jak obliczyć x
6 sie 22:16
rumpek:
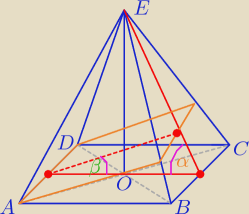
Trochę wyraźniejszy rysunek
i tak jest to trapez równoramienny, x też z tw. sinusów
6 sie 22:24
rumpek:
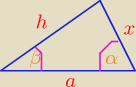
x obliczysz tw. sinusów przy takich oznaczeniach
6 sie 22:26
nikt : ale na twoim rysunku x nie jest drugą podstawą trapezu
6 sie 22:28
rumpek: cwane zadanie, co
? zauważ, że możesz bez problemu obliczyć wysokość ściany bocznej a potem
odjąć ten x u mnie na rysunku i otrzymasz to co chcesz
6 sie 22:29
nikt : czy dłuższa podstawa trapezu wynosi :
6 sie 22:38
rumpek: dłuższa podstawa trapezu to przecież
a
6 sie 22:40
nikt : grrr krótsza
6 sie 22:41
rumpek: nie wiem, napisz całe rozwiązanie
mi ja tam od razu wszystko podstawiałem
właśnie pisze
rozwiązanie jakby co
6 sie 22:42
nikt : | | a | |
ściana boczna = |
| = b |
| | 2cosα | |
oznaczając za c połowę krótszej podstawy mam z twierdzenia Talesa proporcje :
| | (b−x)a | | | | a | | hsinβ | | ( |
| − |
| )a | | | 2cosα | | sinα | |
| | a | |
c = |
| = |
| = . . . |
| − |
| | 2b | | | | 2 | |
| | hsinβcosα | |
to w takim razie krótsza podstawa jest równa 2c = a − 2 |
| |
| | sinα | |
6 sie 22:48
rumpek: wstaw za h, coś
6 sie 22:53
nikt : | | 2 * a * sinα | | sin2αsinβ | |
a − |
| * sinβcosα}{sinα} = a(1 − |
| |
| | sin(α+β) | | sin(α+β)*sinα | |
6 sie 22:56
rumpek:
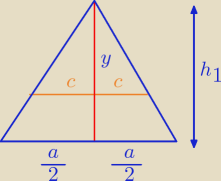
1
o (Tw. sinusów → h)
| h | | a | |
| = |
| |
| sinα | | sin(180o − (α + β) | |
hsin(α + β) = asinα / : sin(α + β)
2
o (Tw. sinusów → x)
| a | | x | |
| = |
| |
| sin(180o − (α + β) | | sinβ | |
asinβ = xsin(α + β) / : sin(α + β)
3
o (War. tryg → h
1)
4
o (Liczymy teraz tę twoją wysokość z rysunku, określmy ją y)
y = h1 − x
| | a | | asinβ | |
y = |
| − |
| |
| | 2cosα | | sin(α + β) | |
| | asin(α + β) | | 2asinβcosα | |
y = |
| − |
| |
| | 2cosαsin(α + β) | | 2cosαsin(α + β) | |
| | a(sin(α + β) − 2cosαsinβ) | |
= |
| |
| | 2cosαsin(α + β) | |
5
o (Liczę z podobieństwa trójkątów c)
| a(sin(α + β) − 2cosαsinβ) | |
| | | 2cosαsin(α + β) | |
| | | |
| = |
| |
| c | | | |
| a2(sin(α + β) − 2cosαsinβ) | | ac | |
| = |
| / * 2cosα |
| 4cosαsin(α + β) | | 2cosα | |
| a2(sin(α + β) − 2cosαsinβ) | |
| = ac / : a |
| 2sin(α + β) | |
| | a(sin(α + β) − 2cosαsinβ) | |
c = |
| |
| | 2sin(α + β) | |
6
o (Pozostało policzyć pole przekroju, przy czym pamiętać, iż górna podstawa to
2c)
| | | | a(sin(α + β) − 2cosαsinβ) | | a + |
| | | | sin(α + β) | |
| | asinα | |
P = |
| * |
| |
| | 2 | | sin(α + β) | |
| | | asin(α + β) + asin(α + β) − 2acosαsinβ | |
| | | sin(α + β) | |
| | asinα | |
P = |
| * |
| |
| | 2 | | sin(α + β) | |
| | 2asin(α + β) − 2acosαsinβ | | asinα | |
P = |
| * |
| |
| | 2sin(α + β) | | sin(α + β) | |
| | asin(α + β) − acosαsinβ | | asinα | |
P = |
| * |
| |
| | sin(α + β) | | sin(α + β) | |
| | asinα(asin(α + β) − acosαsinβ) | |
P = |
| |
| | sin2(α + β) | |
| | a2sinα[sinαcosβ + cosαsinβ − cosαsinβ] | |
P = |
| |
| | sin2(α + β) | |
| | a2sinα*sinαcosβ | | a2sin2αcosβ | |
P = |
| = |
| |
| | sin2(α + β) | | sin2(α + β) | |
ufff
jakieś chochliki być mogą, ale starałem się kontrolować
będzie dla przyszłych
pokoleń
6 sie 22:58
nikt : omg zajmuje więcej miejsca niż wzory Cardano
6 sie 23:05
Eta:
A Ten ciągle o
wzorach Cardano
6 sie 23:08
nikt : Są fajne
6 sie 23:08
Eta:
6 sie 23:09
rumpek:
6 sie 23:10
Saizou : to może zadanko na dobranoc
6 sie 23:12
Eta:
Ejjj
nie rozwiązałeś poprzednich! ......... czekamy
6 sie 23:13
rumpek: Saizou możesz tez wyrazić moje zadanie w tg
6 sie 23:14
Eta:
Dane są zbiory: A = <1; 22012> i B= <22012; 22013>
Który z nich zawiera więcej liczb całkowitych?
Odpowiedź uzasadnij !
6 sie 23:17
Saizou : zbiór A zawiera (22012−1)+1=22012
a zbiór B zwiera (22013−22012)+1=22012(2+1)+1
zatem zbiór B zawiera więcej liczb całkowitych
6 sie 23:27
Eta:
6 sie 23:29
Saizou : mówiłem że pierwszych dwóch się nie tykam bo moje umiejętności nie są jeszcze wystarczające
6 sie 23:30
Saizou : to jeszcze jedno i idę spać
6 sie 23:31
Eta:
Nie używając kalkulatora!
Uzasadnij,że √15+√14 −√13 >4
6 sie 23:33
rumpek: co ty, tak w południe chodzisz spać
?
6 sie 23:33
Eta:
Toż to środek dnia
a Ty do spania ?
6 sie 23:34
Eta:
6 sie 23:34
rumpek:
6 sie 23:34
Eta:
6 sie 23:35
Saizou : (√15+√14)2>(4+√13)2
15+2√15*14+14>16+8√13+13
29+2√210>29+8√13
√210>4√13
210>16*13
210>208
cnu
6 sie 23:41
Saizou : do godziny 0:00 będę. To może jeszcze jakieś
6 sie 23:42
Eta:
Teraz się dobrze wyśpij
.........bo jutro będą trudniejsze zadania
Miłych snów
6 sie 23:43
Saizou : mam się bać?
6 sie 23:44
rumpek: nie
"trzeba się wyluzować"
6 sie 23:46
Saizou : czyli mam się bać
6 sie 23:47
rumpek: bać to się możesz przed maturą ...
... z polskiego
6 sie 23:49
Mila: Hej, witam Was. Załóżcie nowy wątek, bo trudno coś tu znaleźć.
Saizou, widzę, że Cię dręczą.
6 sie 23:50
Saizou : Mila jutro założę nowy wątek do zadań a teraz to już się nie opłaca
oj dręczą, ale i nawet dobrze
6 sie 23:51
Eta:
Witaj
Mila 
6 sie 23:55
rumpek: to masz na odchodne proste zadanie:
Mając podaną nierówność: x4 + ax2 + 1 > 0, podaj wynik dla którego wartość parametru a jest
zawsze prawdziwa dla każdego x∊R.
6 sie 23:55
Eta:
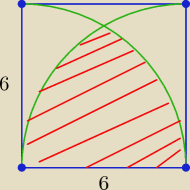
Oblicz pole zacieniowanej
części
6 sie 23:59
Mila: 
7 sie 00:00
Saizou : to do jutra zacznę dzień od rozwiązania tchy zadań w nowym wątku
a teraz mówię wszystkim dobrej nowy
7 sie 00:00
Eta:
7 sie 00:01
rumpek: patrzcie jaki słowny
o
00:00 idzie
Gdyby politycy byli tacy słowni
7 sie 00:02
rumpek:
7 sie 00:02
Eta:
Właśnie tacy są
7 sie 00:02
Saizou : to żeby już jedno mieć z głowy to a∊(−2:+∞)
Dobranoc
7 sie 00:02
7 sie 00:04
rumpek: ale co ma być
?
7 sie 00:06
Eta:
0:0
7 sie 00:06
nikt : może pomyślał że jak zawinie do wzoru skróconego mnożenia to skończy zadanie
7 sie 00:07
7 sie 00:07
rumpek: 
7 sie 00:08
Eta:
7 sie 00:09
pigor: ... no to wyszło mi pole=
3(4π−3√3) , dobranoc . ...
7 sie 01:15
konrad: ja mam pytanie do tego zadania podanego przez rumpka o 23:55
w poleceniu jest "podaj wynik...", ale jaki wynik? rozumiem, że nie chodzi tu o 'a', o 'x' też
nie bo jest powiedziane, że x∊R, czyli co trzeba podać
7 sie 09:06
rumpek: to co podał
Saizou
7 sie 09:55
konrad: czyli jednak a? jakoś dziwnie mi brzmi treść tego zdania
7 sie 09:56
Bogdan:
Dla mnie treść zadania:
Mając podaną nierówność: x4 + ax2 + 1 > 0, podaj wynik dla którego wartość parametru
a jest zawsze prawdziwa dla każdego x∊R
też jest niejasna (co to znaczy, że a jest prawdziwe?)
A może powinno być tak:
Mając podaną nierówność: x4 + ax2 + 1 > 0, podaj wartość parametru a∊R, dla którego ta
nierówność jest zawsze prawdziwa dla każdego x∊R
7 sie 11:15