Zabaweczki Maslanek: To i ja proszę o jakieś ciekawe zadanka z algebry (byle bez modulo )

Mila: Jaki poziom? Indukcja może być?

Mila: Udowodnij,że dla każdej liczby naturalnej

1		1		1		1
	+		+		+...............		=U{n}2n+1}
1*3		3*5		5*7		(2n−1)(2n+1)

Mila:

	n
P=
	2n+1

Mila: Zadanie 2. Rozwiąż równanie:

	1		1		1
1+		+		+		+.........=1−2x
	1−x		(1−x)2		(1−x)3

Eta: Zad.3/ Wykaż,że dla każdej liczby naturalnej m > 2 zachodzi równość: log₃2*log₄3*log₅4*log₆5*.... *log_m+1(m )= log_m+1(2)

Tomek.Noah: Hmm do zadania Ety to chyba można indukcją albo skorzystać z własności log_ba*log_cb=log_cb^log_ba=log_ca

Maslanek: 1. Dla n=1:

	1		1
L=		; P=
	3		3

2. Niech k∊N₊ oraz n≥k

	1		1		1		k
Zał. ind.:		+		+15*7+...+		=
	1*3		3*5		(2k−1)(2k+1)		2k+1

	1		1		1		1		k
Teza:		+		+15*7+...+		+		=
	1*3		3*5		(2k−1)(2k+1)		(2k+1)(2k+3)		2k+3

	k		1		2k2+3k+1
Dowód: Lt = (zał.)		+		=		=
	2k+1		(2k+1)(2k+3)		(2k+1)(2k+3)

	(2k+1)(k+1)		k+1
=		=		.
	(2k+1)(2k+3)		2k+3

Indukcja kończy dowód.

Mila:

	k+1
W tezie − prawa strona powinna być:		ale to chyba błąd przy przepisywaniu, bo to
	2k+3

właśnie udowodniłeś.

Maslanek: Zad. 2. Lewa strona to szereg geometryczny.

	1		1		1
Zbieżny, gdy |		|<1 ⇔		<1 oraz		>−1 ⇒ 1−x<1 oraz 1−x>−1 ⇒ x>0 oraz x<2.
	1−x		1−x		1−x

	1−x		1−x
L=		= −		.
	1−x−1		x

	1−x
−		= 1−2x (x≠0)
	x

x−1=x−2x² 2x²−1=0

	√2
x=±
	2

Powinno grać, ale trochę późno. Etuś, jutro

Mila: W zadaniu Ety − tylko własności logarytmów.

Mila: Maslanek błąd w pierwszej linijce, błędnie rozwiązane nierówności.

Eta:

Eta: @ Maślanek co do zad.3 ........ ja mam czas, ja poczekam

Mila: Dobranoc

Maslanek: Ło Boże Nieźle rozwiązane te nierówności xD Poprawka 1−x<(1−x)² ⇒ (1−x)(1−x−1)>0 ⇒ x(x−1)>0 ⇒ x∊(−∞, 0)∪(1,∞) 1−x>−(1−x)² ⇒ (1−x)(1−x+1)>0 ⇒(x−1)(x−2)>0 ⇒ x∊(−∞,1)∪(2,∞). Zatem x∊(−∞,0)∪(2,∞) To natomiast odrzuca jedno z rozwiązań (dodatnie).

Maslanek: log32*log43*log54*log65*.... *logm+1(m )= logm+1(2) 1. Dla m=3

	log42		1
L=log32*log43=		*log43=
	log43		2

	1
P=log42=		.
	2

2. Niech n≥k, k∊N, k≥3. Zał. ind.: log₃2*log₄3*log₅4*log₆5*.... *log_m+1m= log_m+12 Teza. ind.: log₃2*log₄3*log₅4*log₆5*.... *log_m+1m*log_m+2m+1= log_m+22 Dowód: L= log₃2*log₄3*log₅4*log₆5*.... *log_m+1m*log_m+2m+1 = (zał.) log_m+12*log_m+2m+1 =

	logm+22
=		*logm+2m+1 = logm+22 = P.
	logm+2m+1

Korzystając z zasady indukcji matematycznej wykazaliśmy, że równanie jest tautologią dla każdej liczby naturalnej większej od 2.

Maslanek: Tak swoją drogą, to coś takiego podśrubowanego

Maslanek: Poproszę się znaczy

Trivial: Maslanek, log₃2*log₄3*log₅4*...*log_m+1m =

	log(2)		log(3)		log(4)		log(m)
=		*		*		*...*
	log(3)		log(4)		log(5)		log(m+1)

	log(2)
=		= logm+1(2).
	log(m+1)

Maslanek: Z klawiaturą zajmuje tyle samo czasu (ctrl c )

Trivial: Maslanek, zadanko ode mnie − gra w zgadywanie. Dany jest ciąg (1, 2, 3, 4, 5, ..., 131071, 131072). Jedna osoba wybiera liczbę n z tego ciągu. Druga osoba próbuje zgadnąć n, ale może zadawać tylko pytania postaci: czy n<2? czy n>5? ... itp. Będąc drugą osobą, jaka jest minimalna liczba pytań, które musisz zadać, aby mieć pewność że znalazłeś n. Uwaga: Twój przeciwnik nie gra uczciwie!! Próbuje zawsze wydłużyć proces poszukiwania. Podczas gry może zmieniać n, ale tylko tak, żeby zgadzało się ze wszystkimi wcześniejszymi pytaniami.

Maslanek: Opłaca się zadawać pytania z środkami. Potrzeba 2¹⁶ prób

Trivial: Nie. Znacznie, znacznie mniej.

picia: 16?

Trivial: Dlaczego 16? Podpowiedź: 131072 = 2¹⁷

picia: to 17?

Trivial: Tak.

picia:

Maslanek: Wiem. To zauważyłem Ale potrzeba jednego pytania mniej. Bo jeśli zadam czy to 2? a będzie 1, to odpowiedź już mam. W sumie racja z tą 2¹⁶. Bezmózg totalny −,−

picia: 8= 2³ czy n>4? nie czy n>2? 1)tak czyli zostaja 2 mozliwosci albo 3 albo 4 wiec trzeba zadac kolejne pytanie 2) nie tez zostaja dwie mozliwosci. albo 1 albo 2 wiec trzeba zadac 3 pytania PS a pytania moga byc tylko czy n>... badz n<...

Maslanek: W sumie racja Next one

picia: mam nadzieje ze Ci nie popsulem zagadki no ale to bylo silniejsze ode mnie

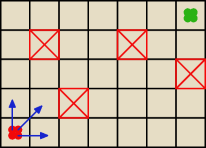
Trivial: To może to, co dałem ostatnio, ale troszkę zmienione. Jesteś królem na szachownicy. Oblicz ile jest możliwości przejścia szachownicy 5x7 wychodząc z czerwonego pola idąc w kierunku zielonego. Nie można się cofać − dozwolone jest tylko chodzenie w górę, w prawo i po skosie (patrz rysunek). Dodatkowo, nie można przechodzić przez przekreślone pola.

Maslanek: Z tymi Twoimi rozrywkami

Maslanek: Eee.. Wyszło mi 50 możliwości

Maslanek: 27 możliwości przejścia dołem 3 możliwości przejścia górą (idąc do góry) 8+24 możliwości przejścia środkiem

Trivial: Za mało.

Maslanek: Dużo za mało? 53 teraz

Maslanek: Albo w sumie koło 60 (bo doliczyłem tylko jeden przypadek )

picia: czy da sie to jakos policzyc matematycznie a nie recznie ?

Trivial: Ja liczyłem ręcznie. Wyszło mi więcej niż dwieście.

picia: To Maslanek dal troche za malo... a w poprzednim z szachami widzialem ze Artur.. to jakos policzyl, tamto tez Trivial liczyles recznie?

Trivial: Tak. To jest pewien sposób, wcale nie trudny.

picia: ponad 200...hmm ciekawe jak sie nie pogubic

Trivial: Właśnie chodzi o to, żeby znaleźć sposób, żeby się nie pogubić. A sposób jest naprawdę prosty. Wymaga jedynie sprawnego dodawania nie więcej niż trzech liczb na raz.

konrad: dla Ciebie Trivial to chyba wszystko jest proste

Saizou : Trivial ale po skosie tylko w górę?

Trivial: Tak. Po skosie w górę.

Trivial: dozwolone tylko 3 ruchy.

Artur z miasta Neptuna: ojjj Trivial −−− Ty to lubisz ludziom utrudniać życie. Rozwiążę to (na razie) bez opcji punktów 'niedozwolonych':

	10 4
Przejścia bez ruchów po skosie:		= 210 sposobów

	9 1		8 3
Z jednym 'po skosie'		*		= 504 sposobów

	8 2		6 2
Z dwoma 'po skosie'		*		= 420 sposobów

	7 3		4 1
Z trzema 'po skosie'		*		= 140 sposobów

	6 4		2 0
4 razy 'po skosie'		*		= 15 sposobów

Trivial: Dobry wynik, ale miała być wersja z przeszkodami.

Mila: Maslanek − 10:01 OK i patrz Trivial 10:20

Artur z miasta Neptuna: A teraz dorzucając punkty 'niedozwolone' Bez skosów: Od wyniku należy odjąć:

4 3		6 1
	*		−−−− przejście przez punkt (2,4) −> czyli otrzymanie sekwencji "GGGP" i jej

permutacji

3 1		7 3
	*		−−−− przejście przez punkt (3,2)

7 3		3 1
	*		−−−− przejście przez punkt (5,4)

8 2		2 2
	*		−−−− przejście przez punkt (7,3)

Następnie należy dodać:

4 3		3 0		3 1
	*		*		−−− przejście przez punkt (2,4) oraz (5,4) −−−dwukrotnie odjęty powyżej

3 1		4 2		3 1
	*		*		−−− przejście przez (3,2) oraz (5,4)

3 1		5 1		2 2
	*		*		−−− przejście przez (3,2) oraz (7,3)

Podobno (ale trochę bardziej skomplikowaną) procedurę należy powtórzyć dla następnych etapów 'skośnych przejść'

Artur z miasta Neptuna: Trzeba to na spokojnie sobie porozpisywać (jakie ruchy doprowadzą do 'wejścia' w punkt niedozwolony) i poodejmować ... nie jest to trudne ... ale szczerze −−− nie chce mi się tego pisać

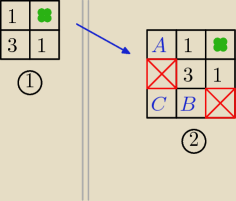
Trivial: To może napiszę jak ja rozwiązałem. Najpierw rozwiązałem to zadanie dla małego rozmiaru szachownicy − 2x2. Taki problem rozwiązać potrafi każdy (rysunek 1). Liczby w kwadratach oznaczają ilość możliwości przejścia szachownicy startując w tym polu. Następnie zwiększamy troszkę rozmiar problemu (rysunek 2). Dla A możemy iść tylko w prawo, więc jest tylko jedna możliwość. A=1. Dla B możemy iść albo w górę, albo po skosie. Zatem B = 3 + 1 = 3+1 = 4. Dla C możemy iść albo po skosie, albo w prawo. C = 3 + B = 3 + 4 = 7.

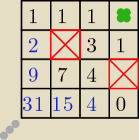
Trivial: Postępując w ten sposób wypełniamy tabelkę do końca.

Maslanek: Twoim sposobem wyszło mi 210 Szkoda, że swoją karteczkę wyrzuciłem. Czegoś może bym się dowiedział

Trivial: Wynik to 242, próbuj dalej.

niuans: a mnie ciągle wychodzi 252

niuans: a nie 242 heheh fajna zabawa

Maslanek: Wychodzi 242. W tym samym miejscu dwa razy wpisałem to samo

Maslanek: To może coś trudniejszego od indukcji, ale do liczenia?

Trivial: Zadanie: wyprowadź wzór na sumę ciągu geometrycznego.

nikt : To zadanie z tym wzorem to dla mnie ?

Trivial: nikt, dla Ciebie za proste. Wystarczy coś zauważyć. Ale jeśli chcesz to dawaj.

Trivial: podkreśliłem Cię.

nikt : Dam najpierw pomyśleć Maslankowi Ogólny schemat rozwiązania mam już w głowie

Maslanek: Za 1,5h pomyślę

Maslanek: Dobra... Mam

1−qn
	= qn−1+qn−2+qn−3+...q2+q+1.
1−q

A przecież suma kolejnych wyrazów to: a₁(1+q+q²+...+qⁿ⁻¹). Q.E.D

Trivial: Właśnie skorzystałeś ze wzoru, który miałeś wyprowadzić.

nikt : xD

Maslanek: Pokazałem skąd się bierze. Więc nie

Trivial: Dam wskazówkę. Przedstaw q^k jako różnicę dwóch wyrażeń, tak aby po zsumowaniu zostały tylko wyrazy skrajne, a reszta się zredukowała.

Maslanek: A nie mogę wyprowadzić wzór na n wyrazów na biegu? a₁ + a₂ + a₃ + ... + a_n = temu na górze. A wynik dzielenia jest taki jak pokazałem. Czemu nie można tak?

Trivial: Można, ale miałeś ten wzór wyprowadzić, a nie zrobić na nim reverse engineering.

Trivial: To może inne zadanie − trudniejsze, ale do zrobienia. Udowodnij, że:

	n 0		n 1		n 2		n n
(a+b)n =		anb0 +		an−1b1 +		an−2b2 + ... +		a0bn.

nikt : Trivial trzeba poprzez indukcje?

Trivial: Można.

nikt : Przez indukcje to zrobię Ciekawi mnie ten drugi sposób

Trivial: Nie wiem jaki jest inny sposób. Ale na pewno jest. Powiedziałem 'można', bo wiem że można.

Maslanek:

k+1 0		k+1 1		k+1 2		k+1 k
	ak+1b0 +		akb1 +		ak−1b2 + ... +		abk +

	k+1 k+1
		a0bk+1 =

	k+1 0		k 0		k 1		k 1
=		ak+1b0 + (		akb1 +		akb1) + (		ak−1b2 +

	k 2		k k−1		k k		k+1 k+1
		ak−1b2) + ... + (		abk +		abk) +		a0bk+1 =

	k+1 0		k 1		k 2		k k
= (zał.)		ak+1b0 + (		ak−1b2 +		ak−1b2) ..( +		abk) +

	k+1 k+1
		a0bk+1 + (a+b)k = ...

Coś tu nie gra? −,−

Maslanek: Coś nie gra... Źle wykorzystane założenie

Maslanek: Kiedyś już to sobie udowadniałem. Właśnie rozbijając symbole Newtona... Pomyślę po kolacji

Jack: podobne do tego z kwadratami miałem kiedyś na procesach stochastycznych... Stąd to wziąłeś, Trivial?

Trivial: Jack, to przykład programowania dynamicznego. Miałem coś w tym rodzaju na algorytmach. Bardzo fajny sposób, aby rozwiązywać szybko problemy, dla których można znaleźć zależność od tych samych problemów, ale o mniejszym rozmiarze (coś w rodzaju rekurencji).

Maslanek: Coś nie pyka... Nie wiem Może jutro

Jack: thx

Aga1.:

	1−qn
Sn=a1*		, q≠1
	1−q

S_n=a₁+a₂+a₃+...a_n −−−suma początkowych wyrazów ciągu geometrycznego. S_n=a₁+a₁q+a₁q²+...+a₁qⁿ⁻¹ Gdy a₁=1, to S_n=1+q+q²+...+qⁿ⁻¹ i qS_n=q+q²+q³+...+qⁿ. Odejmując równania stronami mamy S_n−qS_n=1−qⁿ S_n(1−q)=1−qⁿ,

	1−qn
czyli Sn=
	1−q

Trivial: Brawo Aga1.

Maslanek: Przecież to jeden pies, co zrobiła Aga i ja Jeśli chodzi o wzór dwumianowy To mamy:

n+1 0		n 0		n 1		n 1		n 2
	an+1b0 + [		anb1 +		anb1] + [		an−1b2+		an−1b2] +

...

	n n−1		n n		n+1 n+1
... + [		a1bn+		a1bn] +		a0bn+1 =

	n k
= (wyrzucamy b przed nawias we wszystkich składnikach sumy ∑ (k=0, n)		an−kbk+1,

	n k		n+1 n+1
czyli mamy: b*∑ (k=0, n)		an−kbk = b*(a+b)n. (mamy też, że		a0bn+1 =

	n n
b*		a0bn.

	x 0		x−1 0		n+1 0		n 0
Dalej:		=		, więc		an+1 zapisujemy jako		an+1

	n k
Wyrzucamy a przed nawias we wszystkich składnikach sumy ∑ (k=0, n)		an−k+1bk, mamy

	n k
więc: a*∑ (k=0, n)		an−kbk = a*(a+b)n.

Ostatecznie sumując to mamy: a*(a+b)ⁿ + b*(a+b)ⁿ = (a+b)ⁿ(a+b) = (a+b)ⁿ⁺¹. Dziękuję

Maslanek: Wpadłem na to całkiem przypadkiem Po prostu odpalałem komputer i w tym samym momencie zapaliła się lampka

Trivial: Za dużo niedomówień Maslanku. Nie czytam.

Maslanek: Jakich niedomówień? Co chcesz wiedzieć?

Trivial: Po prostu mi się nie chce wyszukiwać wzorca w tym co tam jest napisane i mnie to ciągle zbija z tropu. Sam dowód wiem jak wygląda i prawdopodobnie zrobiłeś to samo.

Maslanek: Za dużo pisania by było, gdyby chcieć to pogrupować Daj coś następnego

Trivial:

	1 1 1 0		fn+1 fn fn fn−1
Udowodnij, że		n =		, gdzie fn to n−ta liczba

Fibonacciego.

Trivial: Dla ścisłości:

	⎧	n dla n < 2
fn =	⎨
	⎩	fn−1 + fn−2 dla n ≥ 2

Maslanek: Nie rozumiem zapisu mógłbyś przybliżyć?

Trivial:

	1 1 1 0
To macierze są. Podnosimy macierz		do n−tej potęgi.

Maslanek: Niespecjalnie mam pojęcie jak to się robi, ale zobaczymy co z tego wyjdzie L: W=0−1=−1; Wⁿ=1, gdy n=2k lub Wⁿ=−1 dla n=2k+1. P: W=f_n+1*f_n−1−f_n²=(f_n−1+f_n)*f_n−1−f_n² = f_n−1²+f_n*f_n−1−f_n² = f_n−1²+f_n(f_n−1−f_n) = f_n−1² + f_n−1(f_n−1−f_n−1−f_n−2) + f_n−2(f_n−1−f_n−1−f_n−2) = = f_n−1² − f_n−1f_n−2 − f_n−2² = (f_n−1+f_n−2)(f_n−1−f_n−2) − f_n−1f_n−2 = ... Idę w ogóle właściwym tropem?

Godzio: Przeprowadź zwykły dowód indukcyjny Pokaż, że

1 1 1 0		fn + 1 fn fn fn − 1		fn + 2 fn + 1 fn + 1 fn
	*		=

Godzio: A to, że wyznaczniki były by równe to nie oznacza, że macierze są równe Przykład:

	1 1 1 0
|		| = −1

	2 1 5 2
|		| = −1

	1 1 1 0		2 1 5 2
Ale		≠