przytulaj nikt : Eta mogę prosić o jakieś fajne zadanko? Tylko nie z prawdopodobieństwa

Artur z miasta Neptuna: Dany jest ostrosłup prawidłowy czworokątny ABCDS . Punkt M jest środkiem wysokości tego ostrosłupa. Niech x równa się odległości punktu M od krawędzi bocznej ostrosłupa, a y równa się odległości punktu M od ściany bocznej tego ostrosłupa. a. Wyznacz objętość ostrosłupa w zależności od x i y oraz sprawdź, czy istnieje ostrosłup, w którym x = 2 ∧ y = 1. b. Oblicz cosinus kąta między wysokościami sąsiednich ścian bocznych, poprowadzonymi z wierzchołka S ostrosłupa. Zadanie maturalne (z dawnych lat)

nikt : Czyli x oraz y są wysokościami trójkątów prostokątnych ? Dobrze ja to rozumiem?

Eta:

nikt : dajcie jakąś podpowiedź Rysunek dobry do tej podpowiedzi też sie przyda

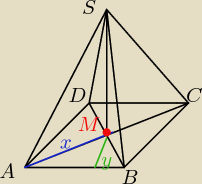
Saizou : mnie się wydaje że coś takiego

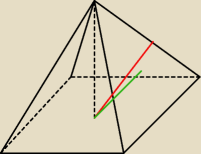
nikt : czerwony − x zielony − y

Godzio: Nie spodkiem, a środkiem Nie ma co dawać podpowiedzi, za 4 h możesz poprosić o podpowiedź, to będzie dobry czas na myślenie

rumpek:

Eta:

nikt : Godziu nie pomagasz

rumpek: ISCP w ogóle na twoim rysunku nie ma punktu M (który jest ŚRODKIEM wysokości tego ostrosłupa)

nikt : środkiem a nie spodkiem xD

rumpek:

Godzio: Zadanie nie jest trudne Rysuj sobie przekroje, z "iksem" i "igrekiem", trochę rachunków i koniec

Artur z miasta Neptuna: Punkt M jest środkiem wysokości tego ostrosłupa Dlaczego M traktujecie jako środek kwadratu

Artur z miasta Neptuna: Godzio −−− toć to zadanie maturalne ... a zadania maturalne nigdy nie były trudne ... trzeba było tylko trochę rachunków i 2 strony opisywania 'skąd co się wzięło'

Godzio: No mi właśnie sporoooooo rachunków wyszło Wynikami się nie chwale bo chodziło mi o sam fakt obliczenia, a nie sprawdzałem czy nigdzie się nie pomyliłem

Patryk: skorzystałeś z podobieństwa trójkątów prostokątnych ?

Godzio: Jeśli to do mnie pytanie to tak

rumpek: każdy chyba z tego skorzystał

Patryk:

nikt : to nie mój poziom Możecie wrzucić rozwiązanie.

Eta: Maturę zdałeś

nikt : Jak widać miałem szczęście.

Eta: Dokładnie

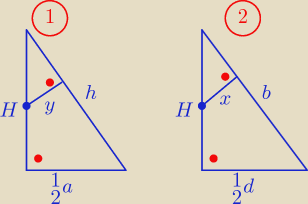
Godzio: H − wysokość ostrosłupa h − wysokość ściany bocznej a − krawędź podstawy b − krawędź boczna d − przekątna podstawy Rób łosiu (tylko nie pomyl się, trójkąty 1 i 2 nie są podobne)

nikt :

	2√2xy
H =
	√2y2−x

	4√2x
a =
	√x − 2y2

Czy chociaż jedno z tych jest dobrze ? Obydwa oczywiście być nie mogą.

Mila: Zadanie dla Nikt Wyznacz taką liczbę a, żeby funkcja

	1		π
f(x)=a sinx+		sin3x miała ekstremum lokalne w punkcie x=		.
	3		3

Następnie zbadaj, czy to jest maksimum czy minimum.

nikt : Mila do tego zadania trzeba znać pochodne ?

ZKS: Raczej tak.

Mila: Tak.

Mila: Zadanie 2. Rozwiąż równanie:

	1		1		1
1+		+		+		+.........=1−2x
	1−x		(1−x)2		(1−x)3

ZKS: Suma nieskończonego ciągu geometrycznego gdzie:

	1
a1 = 1 ∧ q =
	1 − x

nikt : Ja jeszcze nie miałem pochodnych

Mila: No to masz zadanie 2. Co miałeś na algebrze? Na analizie?

rumpek: a może chcesz zadanie związane ze stereometrią ?

nikt : nie Nie nakładajcie na mnie za dużo zadanek na raz

nikt : Na razie pan Godzio będzie minie z tym ostrosłupem męczył.

ZKS: To ja sobie zrobię jeżeli można to z ekstremum?

Godzio: Czemu ja ? To nie ode mnie zadanko, ja dałem tylko wskazówkę Poczekamy na eksperta to oceni Twoje wyniki W między czasie możesz robić inne zadania

nikt : ZKS ekstremum jest twoje

ZKS: Dziękuję. f'(x) = acos(x) + cos(3x)

	π
acos(		) + cos(π) = 0
	3

1
	a − 1 = 0 ⇒ a = 2
2

	1
f(x) = 2sin(x) +		sin(3x)
	3

f''(x) = −2sin(x) − 3sin(3x)

	π		2√3		π
−2sin(		) − 3sin(π) = −		< 0 Więc w punkcie		jest maksimum.
	3		2		3

ZKS: Heh jak fajnie zapisałem powinno być −√3.

Mila: ZKS − zgadza się.