?
Patryk: zaznacz w ukladzie wspulzednych zbiór wszystkich punktów (x,y),których wspolżędne spełniaja
nierownosc logxy≥0 nie mam zielonego pojęcia , pomorzecie od podstaw ?
3 sie 13:36
Eta:
współ
rzędne !
Dziedzina : x>0 i x≠1 i y>0
Rozpatrz przypadki:
1/ dla x€(0,1) −−f. logarytmiczna malejąca
i z def. logarytmu
y
≤ x
0 ⇒y ≤ 1
2/ dla x>1 −− f. logarytmiczna rosnąca
to: y ≥ x
0 ⇒y ≥1
teraz maluj wykresy

3 sie 13:46
Eta:
pomo
żecie ! bo poma
gamy

3 sie 13:48
Patryk:
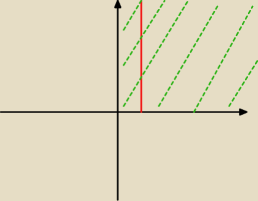
teraz walne dziedzinę, powiesz czy dobrze ?
3 sie 13:49
Patryk: ta czerwona kreska to 1
3 sie 13:50
ZKS:
Wiesz jak wygląda wykres y = 1?
3 sie 13:51
Patryk: tak
3 sie 13:51
ZKS:
To go narysuj.
3 sie 13:53
Patryk:
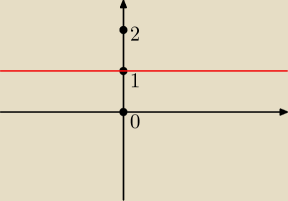
3 sie 13:56
ZKS:
I teraz tak jak napisała Eta rozpatrujesz na dwóch przypadkach
dla x ∊ (0 ; 1) masz y ≤ 1
dla x ∊ (1 ; ∞) masz y ≥ 1
Rysujesz i wszystko zrobione.
3 sie 13:59
ZKS:
Oczywiście pamiętaj o uwzględnieniu dziedziny.
3 sie 14:02
Patryk:
dla x ∊ (0 ; 1) masz y ≤ 1
pzrykład do tego np log1/22=−1 bo 1/2 to liczba z x ∊ (0 ; 1)
dla x ∊ (1 ; ∞) masz y ≥ 1
pzrykład do tego np log24=2 bo 2 to liczba z x ∊ (1 ; ∞)
o to chodzi ?
zaraz to narysuje
3 sie 14:05
Eta:
Dokładnie

3 sie 14:07
Patryk:
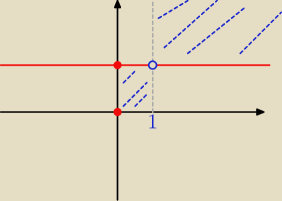
3 sie 14:11
pigor: ... pomo
rzecie

− pomo
żemy

i może ja rozpiszę to tak :
z definicji funkcji logarytmicznej i jej monotoniczności
logxy ≥0 ⇒ (0<x<1 ∧ y>0 i y≤x
0) ∨ (x>1 ∧ y>0 ∧ y≥x
0) ⇔
⇔ (0<x<1 ∧ y>0 i y≤1) ∨ (x>1 ∧ y>0 ∧ y≥1) ⇔
⇔ (
0<x<1 ∧ 0<y≤1) ∨ (
x>1 ∧ y≥1) − szukany opis podzbioru punktów
(x,y) ∊R
2 płaszczyzny XOY , czyli suma punktów wnętrza kwadratu o wierzchołkach
(0,0), (0,1), (1,0) (1,1) bez tych wierzchołków , ale z punktami jego jednego boku
(brzegu) na półprostej y=1 bez punktów (0,1) i (1,1) oraz punktów obszaru opisanego
koniunkcją x>1 ∧ y≥1 i to by było tyle ...

3 sie 14:12
Patryk: musze leciec
3 sie 14:13


 teraz walne dziedzinę, powiesz czy dobrze ?
teraz walne dziedzinę, powiesz czy dobrze ?



 − pomożemy
− pomożemy  i może ja rozpiszę to tak :
z definicji funkcji logarytmicznej i jej monotoniczności
logxy ≥0 ⇒ (0<x<1 ∧ y>0 i y≤x0) ∨ (x>1 ∧ y>0 ∧ y≥x0) ⇔
⇔ (0<x<1 ∧ y>0 i y≤1) ∨ (x>1 ∧ y>0 ∧ y≥1) ⇔
⇔ (0<x<1 ∧ 0<y≤1) ∨ (x>1 ∧ y≥1) − szukany opis podzbioru punktów
(x,y) ∊R2 płaszczyzny XOY , czyli suma punktów wnętrza kwadratu o wierzchołkach
(0,0), (0,1), (1,0) (1,1) bez tych wierzchołków , ale z punktami jego jednego boku
(brzegu) na półprostej y=1 bez punktów (0,1) i (1,1) oraz punktów obszaru opisanego
koniunkcją x>1 ∧ y≥1 i to by było tyle ...
i może ja rozpiszę to tak :
z definicji funkcji logarytmicznej i jej monotoniczności
logxy ≥0 ⇒ (0<x<1 ∧ y>0 i y≤x0) ∨ (x>1 ∧ y>0 ∧ y≥x0) ⇔
⇔ (0<x<1 ∧ y>0 i y≤1) ∨ (x>1 ∧ y>0 ∧ y≥1) ⇔
⇔ (0<x<1 ∧ 0<y≤1) ∨ (x>1 ∧ y≥1) − szukany opis podzbioru punktów
(x,y) ∊R2 płaszczyzny XOY , czyli suma punktów wnętrza kwadratu o wierzchołkach
(0,0), (0,1), (1,0) (1,1) bez tych wierzchołków , ale z punktami jego jednego boku
(brzegu) na półprostej y=1 bez punktów (0,1) i (1,1) oraz punktów obszaru opisanego
koniunkcją x>1 ∧ y≥1 i to by było tyle ... 