Trzy zadanka Lego: Trzy zadanka, bede wdzieczny za pomoc − poziom latwy 1) Trzywyrazowy ciag geometryczny jest rosnacy. Iloczyn wszystkich wyrazow tego ciagu jest rowny −8 a iloraz pierwszego wyrazu przec trzeci wyraz wynosi 2¹₄. Wyznacz ten ciag. 2) Dana jest funkcja wzorem f(x)=3x−5 a) Wyznacz ogolny wyraz ciagu a_n jezeli a₁=f(4), a₂=f(6), a_n=f(2n) b) Uzasadnij ze ten ciag jest ciagiem arytmetycznym c) Oblicz sume wyrazow a₅₀+....a₆₀ 3) Oblicz pole powierzchi trapeza rownoramiennego ktorego przekatna dlugosci "P" tworzy z dluzsza podstawa kat o mierze α

pazio: pomagam

pazio: 1. (a, aq, aq²) geom. ⋀ a≠0 [inaczej iloczyn nie byłby równy jakiekolwiek liczbie] a*aq*aq² = −8 a³*q³ = −8 aq = −2

a		9
	=
aq2		4

1		9
	=
q2		4

	4
q2 =
	9

	2		−2
q =		⋁ q =
	3		3

	−2
dla q =		ciąg nie jest rosnący
	3

	2
q =
	3

	−4
odp (−3, −2,		)
	3

pazio: 2. tu Ci nie pomogę, bo rachunki mi się nie zgadzają i nie ogarniam o co chodzi podpowiedź c) S₆₀ − S₄₉

pazio: 2. tu Ci nie pomogę, bo rachunki mi się nie zgadzają i nie ogarniam o co chodzi podpowiedź c) S₆₀ − S₄₉

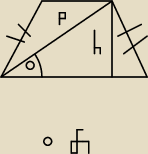
pazio: 3. podstawy trapezu: a,b ⋀ a,b>0

	h
sinα =		⇒ h = p*sinα
	p

	a−b		a+b
druga przyprostokątna: a −		=
	2		2

twierdzenie Pitagorasa w tym samym trójkącie

	a+b
(		)2 = p2 − h2
	2

(a+b)2
	= p2(1 − sin2α)
4

(a+b)² = 4p²*cos²α a+b = 2p*cosα

	1		1
P =		*h*(a+b) =		*p*sinα*2p*cosα = p2*sinα*cosα
	2		2

	1
możesz jeszcze zwinąć do postaci:		*p2*sin2α
	2

Jacek Karaśkiewicz: Drugie zadanie jest nie w porządku. Jeśli a_n = f(2n), to w szczególności a₂ = f(4) = 7, ale ma być a₂ = f(6) = 13, więc jest źle. Może niepoprawnie przepisałeś treść?

Lego: tak jest a₃=f(6) i dalej mi nie bardzo wychodzi z ta suma ciagu

Jacek Karaśkiewicz: Ten ciąg jest źle zdefiniowany (tzn. w tej postaci nie jest to poprawny ciąg). Być może powinno być tak: a₁ = f(2), a₂ = f(4), ..., a_n = f(2n). Wtedy byłoby ok i rzeczywiście ciąg byłby arytmetyczny. A co do sumy a₅₀ + ... + a₆₀ to mielibyśmy tak (gdyby ten ciąg wyglądał tak jak napisałem): r = a_n − a_{n − 1} = f(2n) − f(2n − 2) = 6n − 5 − 6n + 11 = 6 a₁ = f(2) = 1

	2 ⋅ 1 + 59 ⋅ 6
S60 =		⋅ 60 = 10680
	2

	2 ⋅ 1 + 48 ⋅ 6
S49 =		⋅ 49 = 7105
	2

a₅₀ + ... + a₆₀ = S₆₀ − S₄₉ = 3575

Lego: moge wiedziec jak rozpisales ten r? skan zaraz po f(2n)− f(2n−2) = 6n −5 −6n +11 ?

Jacek Karaśkiewicz: Jeżeli ciąg jest arytmetyczny, to definiujemy różnicę ciągu arytmetycznego jako różnicę między dwoma kolejnymi wyrazami (jest to wartość stała dla c. arytmetycznego). Czyli np. r = a_n − a_{n − 1} a_n = f(2n) = 3 * (2n) − 5 = 6n − 5 a_{n − 1} = f(2(n − 1)) = f(2n − 2) = 3 * (2n − 2) − 5 = 6n − 11 a_n − a_{n − 1} = 6n − 5 − (6n − 11) = −5 + 11 = 6 = r