pytanie Krzysiek :D: czy jest możliwość dodania kilku zadań i o rozwiązanie ich w całości ? pozdrawiam Krzychu

Artur_z_miasta_Neptuna: możliwość jest ... natomiast pytanie brzmi −−− czy Ciebie interesuje tylko i wyłącznie całkowicie rozwiazane zadania ... czy może chcesz jedynie naprowadzenie (lub częściowo rozwiązane zadania), abyś nauczył się procedury − sposobu podejścia do problemu

Krzysiek :D: tak interesuje mnie tylko i wyłącznie całkowite rozwiązanie zadania

Krzysiek :D: będę wdzięczny bardzoooo!

Artur_z_miasta_Neptuna: to wrzucaj ... pewnie ktoś rozwiąże ... ale nie zdziw się, jeśli ktoś nie doprowadzi przekształceń do samego końca pisząc '...' lub 'a teraz dokończ sam'

Krzysiek :D: więc pisze 1) Znajdź miejsce zerowe podanej funkcji (jeśli istnieją) : a)y= (x−2) (x+3) b) y = −2x² + 5x −2 2) Narysuj wykres funkcji y = (x−1 )² + 2 3) Znajdź współrzędne wierzchołka paraboli y = x² − 14x+49 i zapisz jej wzór w postaci kanonicznej. Znajdź współrzędne punktu przecięcia wykresu osią oy i narysuj ten wykres. Proszę bardzo o calkowite rozwiązanie

Saizou : 1) a) jest to wzór funkcji kwadratowej zapisanej w postaci iloczynowej y=(x−x₁)(x−x₂), zatem miejscami zerowymi tej funkcji są x₁=2 i x₂=−3 b) licząc Δ możemy to obliczyć Δ=25−16=9 √Δ=3

	−5−3		−8
x1=		=		=2
	−4		−4

	−5+3		−2		1
x2=		=		=
	−4		−4		2

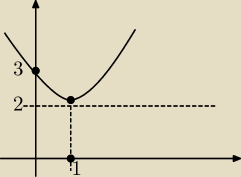
Saizou : 2) rysujemy wykres funkcji x², następnie przesuwamy go o 1 jednostkę w prawo i o 2 jednostki w górę

Krzysiek:D: Saizou dziękuję Ci bardzo a z 3 poradzi sobie ktoś

Saizou : współrzędne wierzchołka paraboli to:

	−b		14
Xw=		=		=7
	2a		2

	−Δ		0
Yw=		=		=0
	4a		4

Δ=196−169=0 zatem wzór funkcji w postaci kanonicznej to: y=(x−7)² punkt przecięcia z osią Y: y=(x−7)²=49 a rysunek za chwilę wrzucę

Krzysiek:D: jesteś wielki mogę dodawać jeszcze zadania ? czy już na dziś Ci wystarczy ?

Saizou : a wrzuć jak będę umiał to pomogę

Saizou : wykres mi się nie chce wczytać

Krzysiek:D: bedzię bez wykresu

Krzysiek:D: 1) Rozwiąż nierówność a) 3x² > bądź równe 27 b) x² +6x +9 >0 2) Rozłóż na czynniki pierwsze: a) W (x) 9x² −64 b) W (x) 5x³ − 3x² 20x+12 3) Rozwiąż równanie: x³ −x² + 2x = 0

Saizou : a)3x²>27 x²>9 lxl>3 x>3 lub x<−3 x∊(−∞:−3)U(3:+∞) b) x²+6x+9>0 (x+3)²>0 zrób rysunek pomocniczy x∊R\{−3}

picia: w 2) brakuje = i w b) cos chyba nie tak

Saizou : 2) a) korzystam ze wzoru a²−b²=(a+b)(a−b) (9x²−64)=(3x−8)(3x+8) b) grupowaniem tyk 5x³−20x−3x²+12=5x(x²−4)−3(x²−4)=(x²−4)(5x−3)=(x+2)(x−2)(5x−3)

Saizou : 3) x(x²−x+2)=0 x=0 x²−x+2=0 Δ=1−8=−7 brak miejsc zerowych

Krzysiek :D: przepraszam w b się pomyliłem w(x) = 5x³ − 3 x² − 20x +12

Krzysiek :D: teraz da się to b zrobić ?

Saizou : przecież już napisałem rozwiązanie

jok: podpowiedz:" łączysz" 3 i 12 z 5 i 20

jok: a ja nie zauwazylem saizou rozwiązania, sorry za plagiat

Krzysiek:D: jeszcze jedno, bo mam ich dużo a nie chce WAS zamęczać ( chyba że chcecie Wyznacz współczynnik k, tak aby wskazane wielomiany były równe ; f(x)= x³ − 2x² +3x −k g(x) = ( x−2)(x²+3 )

nikt : k = 6

Krzysiek:D: skąd wiadomo,że 6 prosiłem że w miarę możliwości proszę o całe rozwiązanie .

Saizou : G(x)=x³+3x−2x²−6=x³−2x²+3x−6 zatem przyrównując współczynniki k=6

nikt : g(x) = x³ − 2x² + 3x − 6 f(x) = x³ − 2x² + 3x − k sprawdzamy współczynniki przty odpowiednich potęgach : 1 = 1 −2 = −2 3 = 3 −6 = −k ⇒ k = 6

Krzysiek:D: dzieki Wam bardzooooo jestescie wspaniali

b.: > Krzysiek :D: tak interesuje mnie tylko i wyłącznie całkowite rozwiązanie zadania Gratulacje Saizou, rozwiązałeś za kogoś zadanie domowe (lub coś podobnego). Możesz być z siebie dumny.

Krzysiek:D: niech będzie bo jest świetny

b.: Zgadza się, jest świetny i wspaniały.

Krzysiek:D: nie wszyscy rozumieją matematykę tak jak on

Saizou : Panie b. mnie to sprawiło przyjemność a że są wakacje to mało kto ma zadania domowe, a to było dobre powtórzenie wiadomości, a nuż komuś się to mogło przydać, a mi zabiło czas, który spędzam bezproduktywnie w domu

Krzysiek:D: Saizou jutro Ci podeśle parę zadań ( chyba,że uda mi się je rozwiązać ) ! Jesteś WIELKI !

Saizou : wielcy na tym forum to między innymi Eta, Mila, Basia, rumpek, nikt, Artur z miasta Neptuna, Trivial, Gustlik. Ja co najwyżej jestem zwykłym szarakiem na tym forum

b.: no to może Krzysiek Ci objaśni, po co potrzebne mu są rozwiązania tych zadań...

Eta:

Krzysiek:D: Dla mnie WIELKI bo zadania są dosłownie za parę minut gotowe z objaśnieniem i wiem gdzie sam robię błąd , krok po kroku

Krzysiek:D: b. a po co Ci wiedzieć na co są mi potrzebne te zadania ?

Saizou : bo pan be kropka chce udowodnić że miał rację i że jestem łatwo wierny i głupi, że za kogoś lekcje robię

b.: jak dla mnie w takiej sytuacji normalnym postępowaniem jest, że piszesz zadanie i swoje rozwiązanie z prośbą o jego poprawienie (znalezienie błędu) jak ktoś rozwiązał sam zadanie i chce znaleźć błąd, to raczej nie prosi o ,,tylko i wyłącznie całkowite rozwiązanie zadania'' −− jest np. spora szansa, że ,,pomagający'' rozwiąże zadanie inaczej (korzystając z innych wzorów, własności, itp.) i pytający nadal nie będzie wiedział, gdzie był błąd proponuję więc Krzyśku pisanie swoich błędnych rozwiązań, a po paru minutach ktoś pokaże Ci, co należy poprawić

b.: może nie zadanie domowe, tylko np. pracę poprawkową czy coś w tym rodzaju

Krzysiek:D: Nie jesteś ani głupi ani łatwowierny jesli nie dałbym rady rozwiazac kilku zadan jutro to mogę je tu Tobie podesłać?

Krzysiek:D: pytam, bo znów ktoś może pomyśleć ze Cię wykorzystuje

Saizou : tak, ale dla świętego spokoju (mojego i swojego) lepiej wstawiaj również swoje próby rozwiązania

Krzysiek:D: dobra w takim razie w razie potrzeby odezwę się jutro

b.: tu nie chodzi o to, czy mam rację czy nie (w tym przypadku), może i nie, tylko o to, żeby komuś, kto na pytanie takie jak zadał Artur z miasta Neptuna w swoim pierwszym poście odpowiada, że zależy mu na całkowitym rozwiązaniu zadania (a nie ,,nauczenia się procedury − sposobu podejścia do problemu''), nie pisać ot tak kompletnych rozwiązań, a tylko (mimo prośby) rozwiązywać zadanie częściowo, dawać wskazówki, naprowadzać, dawać linki do analogicznych zadań z innymi danymi itp. ale NIE PISAĆ GOTOWYCH ROZWIĄZAŃ

Mila: Krzysiu Argumenty b.: są logiczne, chętnie rozwiążemy Ci Krzysiu zadania, ale lepiej umieszczaj z błędami albo początek, to poprawimy błędy, zadawaj pytania o dalszy ciąg rozwiązania. Czasem umieścimy całe rozwiązanie, gdy będziesz na niewłaściwej ścieżce do wiedzy. Wtedy więcej się nauczysz.

pigor: ...niestety, a ja nie mam czasu i ochoty na naprowadzanie do rozwiązania, krótko mówiąc na naukę tu i teraz kogoś matematyki i nikt (... nie mam ciebie na myśli nikt ) nie będzie uczył mnie dydaktyki (olewam ją i jego nauki przykład − skądinąd sympatyczny pan G ... ) , bo i tak będę pisał swoj "gotowce" mniej lub bardziej udane i niech delikwent wyciąga z nich swoje wnioski i tyle . ... : pozdrawiam .

b.: > ja nie mam czasu i ochoty na naprowadzanie do rozwiązania akurat w najprostszej wersji naprowadzenie do rozwiązania zajmuje mniej czasu niż napisanie całego gotowca −− po prostu piszesz swojego gotowca nie do końca, zostawiając coś do policzenia (nie musisz potem sprawdzać, czy osoba pytająca dokończyła Twoje rozwiązanie, w razie potrzeby na pewno zareaguje inny pomagający) a jeśli zadanie jest standardowe, można szybko znaleźć analogiczne rozwiązane na matematyka.pisz.pl i dać link ani do pierwszego, ani do drugiego nie potrzeba żadnych umiejętności dydaktycznych

Eta: Przekazuję Panom ........ po Pozdrawiam

b.: o już teraz po dwa dziękuję i pozdrawiam

pigor: ... dzięki Eta no i dzięki b , bo przecież fajnie jest różnić się pięknie . ... pozdrawiam i życzę dobra noc (ta spacja ma tam być ) . ...