funkcja kwadratoa zosia co ma poprawkę ;(: największa wartość funkcji kwadratowej f jest równa 9. Liczby 0 i 6 są miejscami zerowymi tej funkcji. Zapisz wzór funkcji f w postaci ogolnej.

Artur_z_miasta_Neptuna: jest to funkcja kwadratowa ... czyli ma postać y = ax² + bx + c ... lub w innej formie y = a*(x−x₁)*(x−x₂) ... gdzie x₁,x₂ są miejscami zerowymi funkcji krok 1: skoro NAJWIĘKSZA wartość to jakaś konkretna liczba to: a<0 krok 2: skoro miejsca zerowe funkcji to 0 i 6, więc y=a*(x−0)(x−6) = a*x*(x−6) = ax² − 6ax krok 3: wzór na współrzędną y_w wierzchołka paraboli dany jest wzorem:

	−Δ
yw =
	4a

gdzie Δ = b² − 4ac = (−6a)² − 4*a*0 = 36a² czyli:

	−36a2
yw =		= −9a
	4a

z zadania wiesz, że y_w = 9 czyli 9= −9a ⇒ a=−1 co się zgadza z uwagą z kroku1. Odpowiedź: funkcja jest postaci y = −x*(x−6)

zosia co ma poprawkę ;(: dziękuje Ci bardzo za całą odpowiedź na zadanie Arturze!

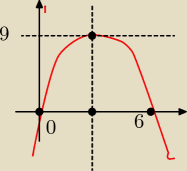
___std_call___: Rysunek koślawy ale od razu wydać, że jeśli f.kwadratowa ma dwa miejsca zerowe to pomiędzy nimi na wykresie leży wierzchołek. Zb. wartości funkcji to oś OY stąd największa wartość to największy Y = 9 − to oznacza, że a < 0. Miejsca zerowe to 0 i 6. Wierzchołek leży pośrodku miejsc zerowych czyli x_wierzchołka to? Z tego masz takie równania: f(x_wierzchołka) = 9 f(0), f(6) = 0

	−b
oraz xw =		gdzie wzór ogólny f.k = ax2 + bx + c.
	2a

pigor: ... lub , z warunków zadania : f(x)=ax(x−6) i x_w=¹₂(0+6)=3 i f(3)=9 ⇒ a*3(3−6)=9 ⇒ −3a=3 ⇒ a=−1, to f(x)= −x(x−6) ⇔ f(x)= −x²+6x − szukany wzór funkcji f w postaci ogólnej .

Aga1.: Lub wystartować od postaci kanonicznej y=a(x−p)²+q Miejsca zerowe

	x1+x2		0+6
x1=0, x2=6, to p=		=		=3
	2		2

Największa wartość, czyli q=9. Do wykresu należy punkt (x₁,0)=(0,0) y=a(x−3)²+9 0=a(0−3)²+9 0=9a+9 a=−1 y=−1(x−3)²+9 −−−postać kanoniczna y=−(x²−6x+9)+9 y=−x²+6x −−postać ogólna

Gustlik: największa wartość funkcji kwadratowej f jest równa 9. Liczby 0 i 6 są miejscami zerowymi tej funkcji. Zapisz wzór funkcji f w postaci ogolnej. Najprościej tak: q=9 x₁=0 x₂=6

	x1+x2		0+6
p=		=		=3
	2		2

Przedstawiam funkcję w postaci iloczynowej: y=ax(x−6) Korzystam z q=f(p) 9=a*3(3−6) 9=a*(−9) a=−1 y=−x(x−6) Odp: y=−x²+6x

pigor: ... po prostu wytłumaczyłeś . ... na swój sposób . ... mój sposób , a ja nie lubię tłumaczyć "gotowca" ... i tyle . ... pozdrawiam