Punkt skupienia Sad: Witam. Mam problem. Mianowicie nie rozumiem definicji punktu skupienia. Jest też mało informacji o nim w internecie. Mógłby mi jakiś pasjonat matematyki wytłumaczyć łopatologicznie co to jest? Znam definicje metryki przestrzennej i zatrzymałem się na punkcie skupienia bo tego nie rozumiem.

Yoyo: dołączam się przy okazji

Artur z miasta Neptuna: punkt skupienia? Ale w odniesieniu do czego? Funkcji? A może zbiorów?

Mila: Zobacz:http://www.matematyka.pl/165759.htm

Artur z miasta Neptuna: punkt skupienia −−−− łopatologicznie jeżeli znajdziesz taki podciąg ciągu (lub ciąg ze zbioru), który będzie dążył do granicy G ... to punkt G jest punktem skupienia. Jedyne założenie −−− ciąg (czy też podciąg) nie może mieć jednakowych wyrazów (nie może być to ciąg stały)

Sad: zbiorow

Sad: a jak to wytumaczyc na zbiorach i jak okreslic kiedy taki zbior jest domkniety lub otwarty?

nikt : z tego co napisał Artur : punkt skupienia jest to zbiór złożony z granic podciągów

Sad: hmmmm....co to jest podciąg? i skąd się wziął podciąg kiedy mówilem że podchodzę do tego od strony przestrzeni metrycznej ? znam conajwyzej pojęcie kuli. Zdąrze przerobić to na studiach teraz potrzebuje tego żeby przejsc do przestrzeni euklidesowej

nikt : Granice ciągów już potrafisz liczyć ?

Vizer: Hello everyone. Widzę, że ciężko się Wam z matmą rozstać, nawet na wakacjach katujecie zadanka

Vizer: Ale jemu nikt chodzi o pojęcie w przestrzeni metrycznej, czyli o zbiory, a nie o ciągi.

nikt : Hmm takiego nie znam jeszcze

Mila: Jutro napiszę, podam przykład.

Sad: dzieki Mila w takim razie czekam

Artur_z_miasta_Neptuna: Vizer −−− a w innych przestrzeniach metrycznych ciągów nie ma Tylko w euklidesowej Sad zbiór domknięty, gdy: ∀_n x_n∊D ⋀ lim x_n=g ⇒ g∊D zbiór otwarty? to taki, którego dopełnieniem jest zbiór domknięty. Lub: zbiór otwarty: (nie jestem pewien czy tak to dokładnie wyglądało) ∀_x∊D ∃_r>0 ∀_y∊K(x,r) y∊D gdzie K(x,r) −−− kula o środku w punkcie 'x' i promieniu 'r' kula to pojęcie bardzo względne, o czym się przekonasz przy rozpatrywaniu różnych metryk zbiór domknięty? to taki, którego dopełnieniem jest zbiór otwarty.

Sad: Zauwazylem ze kule nie interpretuje sie doslownie, jest to jakis model o srodku i odcinkach rownie odleglych od srodka ? jak mam rozumiec punkt skupienia s zbioru X i dowolny obszar zawierajacypunkty zbioru E nie bedace punktami s'. wiesz o co mi chodzi?

Artur_z_miasta_Neptuna: za pomocą kuli można by było wyjaśnić punkt skupienia jako: Jeżeli: ∀_r>0 ∃_{x∊X ⋀ x≠y} x∊K(y,r) to 'y' jest (jednym z) punktem skupienia zbioru X

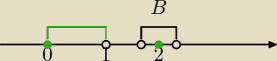
Mila: Punkt x₀ jest punktem skupienia zbioru A⊂R ( R − przestrzeń metryczna) gdy dla każdego δ>0 przedział (x₀−δ, x₀+δ) zawiera punkty zbioru A różne od x₀. Niech A=<0,1)∪{2} (czyli swoimi słowami, każde otoczenie punktu x₀ zawiera punkty zbioru A i te punkty są różne od x₀) Punkt 2 nie jest punktem skupienia zbioru A ponieważ np. dla δ=0,5 przedział B=(2−0,5;2+0,5) nie zawiera żadnego punktu różnego od 2 ze zbioru A. (A\{2})∩B=Φ <0,1> jest zbiorem wszystkich punktów skupienia zbioru A. ( punkt skupienia zbioru nie musi być elementem tego zbioru).

Sad: wielkie dzieki dorwalem podrecznik Franciszka Leji i przyswoje sobie ta cala teorie a reszta na topologii

b.: albo ogólniej, x jest punktem skupienia zbioru A, jeśli x należy do domknięcia zbioru A \ { x }

Sad : Co to znaczy domknięcie zbioru ?

Mila: Tak, wykłady i ćwiczenia z topologii rozjaśnią Ci te problemy i rozwiniesz abstrakcyjne myślenie. Teraz możesz poszukać w internecie materiałów na temat kuli w różnych metrykach.

Artur z miasta Neptuna: domknięcie zbioru A = najmniejszy (w sensie inkluzji) domknięty zbiór zawierający zbiór A np.: domknięciem (−1,1) będzie <−1,1> domknięciem <−1,1) będzie <−1,1> domknięciem <−1,1> będzie <−1,1> 'b' ciekawe spostrzeżenie (chyba nie spotkałem się z nim wcześniej) ... ale chyba trochę niepraktyczne ... zwłaszcza gdy masz wyznaczyć punkty skupienia (bo i tak wtedy korzystać będziesz z pozostałych dwóch metod, zapewne z granicy ciągów) Sad −−− punkty skupienia wykazujesz za pomocą jednej z dwóch metod: 1) granica ciągów (lub też podciągów) 2) kul (na prostej kulę Mila zaprezentowała)

Artur z miasta Neptuna: Sad ... fajnie by było jakbyś gdzieś znalazł stronkę z narysowanymi 'kulami' w różnych metrykach . Kiedyś się 'bawiliśmy' w tworzenie różnych metryk ... kolega tak nakombinował, że przy odpowiednim ustawieniu środka kuli i promienia wychodziła wiśnia z ogonkiem, a po przeniesieniu kuli w stronę osi OX 'kula' zmieniała kształt na gruszkę (bez ogonka) .

Mila: Artur po takich kombinacjach jedna z moich koleżanek zrezygnowała ze studiów, bo stwierdziła , że nie będzie tracić czasu na to, aby jej ktoś wmawiał, że kwadrat jest kulą.

Sad : Tak sobie teraz myślę... Twierdzenie które zaprezentował b. Jest błędne bo punkt skupienia zbioru E może być poza zbiorem E. Np. (rys.) a z tego wynika że jest poza domknięciem tego zbioru

Artur z miasta Neptuna: Sad .... podejrzewam, że u Ciebie kropka robi za punkt skupienia (x). A kwadrat jest zbiorem E. W takim razie zbiór E\{x} = E ... dopełnienie zbioru E to zbiór E ... x∉E ... czyli x NIE JEST punktem skupienia. Sad ... przeanalizuj to spostrzeżenie w 1 wymiarze (na R) dla odcinka (−1,1) ... dla punktów x₁=−1, x₂=0, x₃=1 i x₄=2

Artur z miasta Neptuna: Co więcej ... w ten sposób możesz udowodnić, np.: A={{1},{2},{3}} nie posiada punktów skupienia niech x=1 A\{1} = {{2},{3}} dopełnieniem tego zbioru jest {{2},{3}} ... czyli x nie należy do dopełnienia ... więc nie jest punktem skupienia ... identycznie dla pozostałych punktów. W ten sposób zauważyłeś, że zbiór skończonej ilości punktów izolowanych nie posiada punktu skupienia.

Sad: Czyli jeśli dobrze rozumiem punkt skupiony s zbioru N leży w tym zbiorze LUB na infimum LUB na supremum

Sad: hmmm.. supremum lub infimum pojedynczego przedziału. Bo dla np. (2;8>∪(13;20) mamy punkt skupienia s <2;8>∪<13;20>

Mila: Już się nie włączam do dyskusji, zostaw to na zajęcia topologii. Dobranoc.

Sad: To przynajmniej napiszcie czy dobrze mysle

Artur_z_miasta_Neptuna: tak ... dobrze myślisz. Przy zbiorach odcinków. Co jednak jest punktem skupienia dla zbioru punktów:

	1		1		1
D={1,		,		,		, ... } tutaj sup D = D .... a punkt skupienia będzie leżał
	2		3		4

poza tym obszarem

Artur_z_miasta_Neptuna: tak tak ... straszną głupotę strzeliłem ... wiem wiem

Sad : Supremum = 1 lecz nie jest to punkt skupienia zbioru. Żaden zbiór pojedynczych punktów nie ma punktu skupienia? Mam jeszcze dwa pytania po których dam wam już spokój. Franciszek Lea pisze: 1."Skończony zbiór punktów przestrzeni metrycznej nie ma punktów skupienia." jak to wytłumaczyć? Może ją nie rozumiem co to znaczy skończony zbiór ale zbiór (3;4>. Ma punkt skupienia 2."Zbiór punktów E (znak zawierania) X nazywamy otwartym gdy każdy jego punkt a należy do E wraz z pewnym swym otoczeniem" wyjaśni to ktoś? Byłbym wdzięczny i dał wam spokój

Artur_z_miasta_Neptuna: wpis z 2sie 08:09 ... punktem skupienia zbioru D będzie oczywiście punkt '0' (który nie należy do zbioru D, ale należy do su√D) 1) patrz mój wpis z 1 sie 22:55 dokładnie tego się tyczył 2) innymi słowy: ∀_a∊E ∃_r>0 ∀_b∊K(a,r) b∊E lub inaczej: ∀_a∊E ∃_r>0 b∊K(a,r) ⇒ b∊E a więc wyjaśniasz poprzez kulę −−− w końcu kula prezentuje 'otoczenie' (o odległości r) punktu a

Artur_z_miasta_Neptuna: ciąg dalszy do 1) skończony zbiór PUNKTÓW = zbiór posiadający skończoną liczbę punktów odcinek (3,4> ∼ R ... czyli jest nieprzeliczalny a więc tym bardziej nie jest to skończony zbiór punktów.