Oblicz pole koła wpisanego w romb Klaudia: Oblicz pole koła wpisanego w romb o boku 26cm i przekątnej 4,8dm. Bardzo proszę o pomoc..*

nikt: jest powiedziane która to jest przekątna?

nikt: dobra nie było pytania xD

Kejt: masz może odpowiedź do tego zadania?

nikt:

	14400
P =		cm2
	169

Kejt: więc jednak nie wychodzi ładnie. ok, to wrzucam rozwiązanie..

nikt: 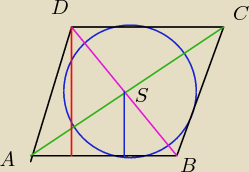niebieski = r − promień okręgu wpisanego czerwony = h − wysokość rombu zielony = d₁ − dłuższa przekątna rombu = 48cm na czarno masz boki = 26 cm na różowo jest krótsza przekątna rombu = d₂ = Wiemy że przekątna dzielą się na połowy i pod kątem prostym więc mamy twierdzenie Pitagorasa w ΔSDC: |SC|² + |SD|² = |CD|²

	d2		d1
(		)2 + (		)2 = |CD|2
	2		2

d22
	+ 576 = 676
4

d₂² = 400 d₂ = 20

	1		1
P = |AC| * |DB| *		= 20 * 48 *		= 480
	2		2

P = |AB| * h 480 = 26 * h

	240
h =
	13

	120
r =
	13

	14400
P =		cm2
	169

ciekawy wynik

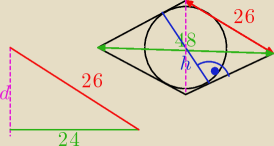
Kejt: d − połowa krótszej przekątnej h − wysokość rombu (i średnica koła) z tw. Pitagorasa: d²=26²−24² d²=676−576 d²=100 d=10 cała krótsza przekątna: 2d=20 ze wzoru na pole:

	48*20
P=		v P=26*h
	2

pole musi wyjść takie samo, więc:

48*20
	=26*h
2

26h=480

	240
h=
	13

	240		1		120
h było średnicą, promień jest dwa razy krótszy, więc: r=		*		=
	13		2		13

P_k=πr²

	14400
Pk=		π
	169

nikt: za wolno

Kejt: przynajmniej nie mam błędu w wyniku..π zeżarłeś

nikt: k%&*a

Kejt: haha!

nikt: głupie to głupie

pigor: ... no to ja, z porównania wzorów na pole trójkąta prostokątnego o wysokości r=? względem przeciwprostokątnej, widzę to tak : ¹₂*2,6 r = ¹₂*2,4√2,6²−2,4² ⇔ r=²⁴₂₆√0,2*5 ⇒ r=¹²₁₃dm , zatem P_k= π r² = ¹⁴⁴₁₆₉π dm² i szukane pole koła . ...

Klaudia: dziękuję Wam ślicznie za rozwiązanie.. Nie, nie było podane , która to przekątna, ale domyślam się, że ta dłuższa, więc jest ok..