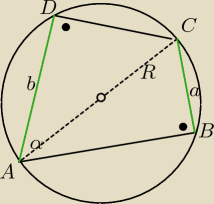
 <B=900,<C=900 − kąty wpisane oparte na średnicy.
<B=900,<C=900 − kąty wpisane oparte na średnicy.
 |AC|= 2R =x ( oznaczam x , łatwiej mi pisać)
|AC|= 2R =x ( oznaczam x , łatwiej mi pisać)
| b | √x2−b2 | |||
z ΔACD : | = cosβ ⇒ sinβ= √1−(b/x)2= | |||
| x | x |
| a | ||
z ΔBAC: | = sin(α−β)= sinα*cosβ−cosα*sinβ | |
| x |
| a | b | √x2−b2 | ||||
zatem: | = sinα* | − cosα* | /*x | |||
| x | x | x |
| (b*sinα−a)2 +b2*cos2α | ||
x2= | ||
| cos2α |
| √b2−2absinα+a2 | ||
x= | ||
| |cosα| |
| 1 | ||
to R= | x =.... | |
| 2 |




 ) :
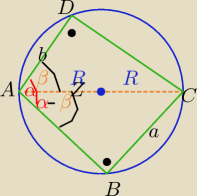
niech na rys. Mila |AC|=2R , |AB|=x , |CD|=y , to z pola czworokąta jako sumy pól
trójkątów i dwukrotnie tw.Pitagorasa :
12(ax+by) = 12[bxsinα+aysin(180−α)] i x2+a2= 4R2 i y2+b2= 4R2 ⇔
⇔ x(a−bsinα) = y(asinα−b) i x2 = 4R2−a2 i y2 = 4R2−b2 ⇔
⇔ (4R2−a2)(a−bsinα)2 = (4R2−b2)(asinα−b)2 − równanie o niewiadomej R=? ⇔
⇔ 4R2[(a−bsinα)2 − (asinα−b)2] = a2(a−bsinα)2 − b2(asinα−b)2 ⇔
⇔ 4R2[(a+b −(a+b)sinα] [(a−b +(a−b)sinα] = (a2−2absinα+b2)(a2−b2) ⇒
⇒ 4R2(1−sinα)(1+sinα) = a2−2ab+b2 ⇒ 4R2cos2α = a2−2absonα+b2 ⇒
) :
niech na rys. Mila |AC|=2R , |AB|=x , |CD|=y , to z pola czworokąta jako sumy pól
trójkątów i dwukrotnie tw.Pitagorasa :
12(ax+by) = 12[bxsinα+aysin(180−α)] i x2+a2= 4R2 i y2+b2= 4R2 ⇔
⇔ x(a−bsinα) = y(asinα−b) i x2 = 4R2−a2 i y2 = 4R2−b2 ⇔
⇔ (4R2−a2)(a−bsinα)2 = (4R2−b2)(asinα−b)2 − równanie o niewiadomej R=? ⇔
⇔ 4R2[(a−bsinα)2 − (asinα−b)2] = a2(a−bsinα)2 − b2(asinα−b)2 ⇔
⇔ 4R2[(a+b −(a+b)sinα] [(a−b +(a−b)sinα] = (a2−2absinα+b2)(a2−b2) ⇒
⇒ 4R2(1−sinα)(1+sinα) = a2−2ab+b2 ⇒ 4R2cos2α = a2−2absonα+b2 ⇒
| a2−2absonα+b2 | √a2−2absinα+b2 | |||
⇒ 4R2 = | ⇒ R= | . ...  | ||
| cos2α | 2|cosα| |

