planimetria
Krzychu:
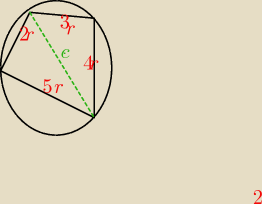
Dany jest czworokąt ABCD wpisany w okrąg. Długośći boków tego czworokąta są kolejnymi wyrazami
ciągu arytmetycznego. Pierwszy wyraz jest równy podwójnej różnicy ciągu. Pole czworokąta jest
równe P=18
√30. Wyznacz różnicę ciągu.
9r
2+16r
2−12r
2cos(180
o−α)=4r
2+25r
2−40r
2cosα
28=40(−cosα)−12cosα
28=−52cosα
Wszystko ok?
27 lip 17:41
Mila: Chyba nie.
Eto , r=3?
boki:6,9,12,15?Jeszcze raz sprawdzę.
27 lip 18:17
Krzychu: tak, r=3. Gdzie u mnie jest błąd?
27 lip 18:22
Krzychu: może ktoś pomóc?
27 lip 18:54
Eta:
Ze wzoru Brahmagupty:
P=
√(p−a)(p−b)(p−c)(p−d)
√2r*3r*4r*5r= 18
√30 ⇒ 120r
4= 18
2*30 ⇒ r
4=81 = 3
4 ⇒
r=3
27 lip 18:58
Krzychu: fajny sposób, tyle że ja chce z tw. cosinusów. Ale ten wzór i tak będzie potrzebny?
27 lip 19:05
Eta:
W Twoim rozwiązaniu powinno być:
29r
2−20r
2cosα= 25r
2+24r
2cosα
dokończ .......... otrzymasz r= 3
27 lip 19:06
Krzychu: ok, ale co teraz

? Bo nie znam żadnego wzoru na pole czworokąta wpisanego w okrąg, poza
wzorem Brahmagupty od teraz. Ale w tym wzorze pojawia się jedno ale.
http://pl.wikipedia.org/wiki/Wz%C3%B3r_Herona#Wz.C3.B3r_Brahmagupty
Dla dowolnego czworokąta (również niewpisanego w okrąg), wzór na jego pole przedstawia się
następująco:.......
(...)W przypadku czworokątów wpisanych w okrąg suma tych kątów jest równa i wynosi 180 stopni.
Końcówka tego wzoru to abcd(cosα)
2 a jak α=180 (w czworokącie wpiosanym w okrąg) to sam
cos180=1 więc w tym wzorze co podałaś powinno być coś jeszcze: −abcd*1 a nie ma.
27 lip 19:11
Eta:
e
2= 4r
2+25r
2−
2*2r*5r*cosα i e
2= 16r
2+9r
2−
2*4r*3r*(
−cosα)
teraz sprawdź, gdzie masz błąd

27 lip 19:11
Krzychu: POŁOWA. Zatem to jest równe 0. Drugie pytanie cofam

.
27 lip 19:12
Eta:
Wartość pola >0
27 lip 19:13
Krzychu: ok ok. Ale wzór Brahmagupty i tak i tak bedzie tu potrzebny?
27 lip 19:18
rumpek:
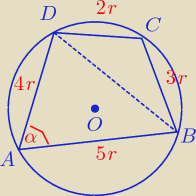
Oznaczmy sobie: te 3 boki są to: a
1, a
2, a
3, a
4 czyli: a
1, a
1 + r, a
1 + 2r, a
1 + 3r
skoro mamy podane, iż: a
1 = 2r. rozpisujemy sobie: 2r, 2r + r, 2r + 2r, 2r + 3r.
Wykorzystujemy wzór na pole Brahmagupty: i otrzymujemy, że
r = 3
|BD|
2 = 16r
2 + 25r
2 − 40r
2cosα
|BD|
2 = 4r
2 + 9r
2 − 12r
2cos(180
−α)
16r
2 + 25r
2 − 40r
2cosα = 4r
2 + 9r
2 + 12r
2cosα
41r
2 − 40r
2cosα = 13r
2 + 13r
2cosα
52cosα = −28
sin
2α + cos
2α = 1
| | 1 | | 2√30 | |
P = |
| * 4r * 5r * |
| = 20r2√30/13 |
| | 2 | | 13 | |
| | 1 | | 2√30 | | 6r2√30 | |
P = |
| * 2r * 3r * |
| = |
| |
| | 2 | | 13 | | 13 | |
| | 26r2√30 | |
P = |
| = 18√30 / * 13 |
| | 13 | |
26r
2√30 = 234
r
2 = 9, r > 0
r = 3
Twoim sposobem

Stay tuned

27 lip 19:18
Eta:
W tym sposobie, który podałeś ,to nie będzie potrzebny

| | 1 | | 1 | |
P(ABCD)= |
| *2r*5r*sinα + |
| *3r*4r*sinα ( sin(180o−α)= sinα |
| | 2 | | 2 | |
| | 2√30 | |
P(ABCD)= ........... dokończ dla sinα= |
| |
| | 11 | |
i otrzymasz ,że r= 3
27 lip 19:22
Eta:
rumpek ja mam w mianowniku
11 
27 lip 19:23
rumpek: a ja 13 i wynik też wychodzi poprawny

27 lip 19:27
Eta:
Nie lubię
13 
27 lip 19:29
rumpek: Tylko,
Eto zauważ że ja mam inne oznaczenia na rysunku niż Krzysio

I tak wyjdzie
poprawnie

A 13 są fajne

szczególnie w piątek

27 lip 19:30
Krzychu: Dzięki. Ale rumpek to samo mam rozwiązanie w książce, tyle że cosinus tam jest dodatni.
27 lip 19:37
rumpek: ZALEŻY OD OZNACZEŃ

27 lip 19:37
rumpek: Zauważcie, że mam inne oznaczenia

27 lip 19:38
Eta:
Ok

27 lip 19:43
Krzychu: nie, popełniłeś błąd w 4 linijce. Wyjdzie dodani. A dodatkowo tam jest 12r
2cosα

27 lip 19:44
rumpek: dobrze jest

mimo, że napisałem 13r
2cosα, a powinno być 12r
3cosα

to potem dodałem 40+12
i wychodzi 52

27 lip 19:46
rumpek: i zauważ, ze jak bedzie dodatni cos to wynik sie nie zmieni

27 lip 19:49
Krzychu: w sensie dobrze jest mówisz że ten cosinus jest ujemny? Może ja jestem ślepy

27 lip 19:51
Krzychu: no wiem wiem, ale w opdowiedziach dają dodatni, a ujemny to mi nie wychodzi. A gdybym tak
przepisał a potem taki (błąd) na maturze dał to może bym stracił 2% a chce mieć równe 100

27 lip 19:52
Mila: Rumpek, zrobiłam też Twoim sposobem.(sposobem Ety też)
cosα>0
27 lip 22:05
pigor: hmm, ... straciłbyś nie 2 % tylko 2 punkty procentowe

. ...

27 lip 22:28
Mila: Powinno być:
−52cos α=−28 (Jest tam błąd rachunkowy)
27 lip 22:31
rumpek: no tak tak

zle przepisany minus

i tyle postów


na maturze bym sprawdzał
chociaz już nie muszę

27 lip 22:59
Krzychu: juz wiem, wyjdzie ujemny cosinus gdy kąt między 4r i 5r nazwiemy (180o−α) a między 2r i 3r α
28 lip 12:03
Mila: Krzychu, chodzi o to, abyś zauważył kąt rozwarty.
Oto zadanie na zrozumienie tego problemu z ujemnym cosinusem. Zastosuj twierdzenie cosinusów.
Wykaż, że w dowolnym równoległoboku suma kwadratów długości przekątnych
jest równa sumie kwadratów długości wszystkich boków.
28 lip 23:44
Marek: aha, czyli że kąt rozwarty trzeba nazywać (180−α) bo rozwarty jest większy od 90 czyli jest w
drugiej ćwiartce, czyli jest ujemny. A ze wzoru jest cos(180−α)=−cosα . Czyli do ostrego to
nie pasuje. Tak?
29 lip 11:19
29 lip 11:22
 Dany jest czworokąt ABCD wpisany w okrąg. Długośći boków tego czworokąta są kolejnymi wyrazami
ciągu arytmetycznego. Pierwszy wyraz jest równy podwójnej różnicy ciągu. Pole czworokąta jest
równe P=18√30. Wyznacz różnicę ciągu.
9r2+16r2−12r2cos(180o−α)=4r2+25r2−40r2cosα
28=40(−cosα)−12cosα
28=−52cosα
Dany jest czworokąt ABCD wpisany w okrąg. Długośći boków tego czworokąta są kolejnymi wyrazami
ciągu arytmetycznego. Pierwszy wyraz jest równy podwójnej różnicy ciągu. Pole czworokąta jest
równe P=18√30. Wyznacz różnicę ciągu.
9r2+16r2−12r2cos(180o−α)=4r2+25r2−40r2cosα
28=40(−cosα)−12cosα
28=−52cosα
 ? Bo nie znam żadnego wzoru na pole czworokąta wpisanego w okrąg, poza
wzorem Brahmagupty od teraz. Ale w tym wzorze pojawia się jedno ale.
http://pl.wikipedia.org/wiki/Wz%C3%B3r_Herona#Wz.C3.B3r_Brahmagupty
Dla dowolnego czworokąta (również niewpisanego w okrąg), wzór na jego pole przedstawia się
następująco:.......
(...)W przypadku czworokątów wpisanych w okrąg suma tych kątów jest równa i wynosi 180 stopni.
Końcówka tego wzoru to abcd(cosα)2 a jak α=180 (w czworokącie wpiosanym w okrąg) to sam
cos180=1 więc w tym wzorze co podałaś powinno być coś jeszcze: −abcd*1 a nie ma.
? Bo nie znam żadnego wzoru na pole czworokąta wpisanego w okrąg, poza
wzorem Brahmagupty od teraz. Ale w tym wzorze pojawia się jedno ale.
http://pl.wikipedia.org/wiki/Wz%C3%B3r_Herona#Wz.C3.B3r_Brahmagupty
Dla dowolnego czworokąta (również niewpisanego w okrąg), wzór na jego pole przedstawia się
następująco:.......
(...)W przypadku czworokątów wpisanych w okrąg suma tych kątów jest równa i wynosi 180 stopni.
Końcówka tego wzoru to abcd(cosα)2 a jak α=180 (w czworokącie wpiosanym w okrąg) to sam
cos180=1 więc w tym wzorze co podałaś powinno być coś jeszcze: −abcd*1 a nie ma.

 .
.
 Oznaczmy sobie: te 3 boki są to: a1, a2, a3, a4 czyli: a1, a1 + r, a1 + 2r, a1 + 3r
skoro mamy podane, iż: a1 = 2r. rozpisujemy sobie: 2r, 2r + r, 2r + 2r, 2r + 3r.
Wykorzystujemy wzór na pole Brahmagupty: i otrzymujemy, że r = 3
|BD|2 = 16r2 + 25r2 − 40r2cosα
|BD|2 = 4r2 + 9r2 − 12r2cos(180 −α)
16r2 + 25r2 − 40r2cosα = 4r2 + 9r2 + 12r2cosα
41r2 − 40r2cosα = 13r2 + 13r2cosα
52cosα = −28
Oznaczmy sobie: te 3 boki są to: a1, a2, a3, a4 czyli: a1, a1 + r, a1 + 2r, a1 + 3r
skoro mamy podane, iż: a1 = 2r. rozpisujemy sobie: 2r, 2r + r, 2r + 2r, 2r + 3r.
Wykorzystujemy wzór na pole Brahmagupty: i otrzymujemy, że r = 3
|BD|2 = 16r2 + 25r2 − 40r2cosα
|BD|2 = 4r2 + 9r2 − 12r2cos(180 −α)
16r2 + 25r2 − 40r2cosα = 4r2 + 9r2 + 12r2cosα
41r2 − 40r2cosα = 13r2 + 13r2cosα
52cosα = −28
 Stay tuned
Stay tuned 




 I tak wyjdzie
poprawnie
I tak wyjdzie
poprawnie  A 13 są fajne
A 13 są fajne  szczególnie w piątek
szczególnie w piątek 




 mimo, że napisałem 13r2cosα, a powinno być 12r3cosα
mimo, że napisałem 13r2cosα, a powinno być 12r3cosα  to potem dodałem 40+12
i wychodzi 52
to potem dodałem 40+12
i wychodzi 52 



 . ...
. ...
 zle przepisany minus
zle przepisany minus  i tyle postów
i tyle postów 
 na maturze bym sprawdzał
chociaz już nie muszę
na maturze bym sprawdzał
chociaz już nie muszę 