CD moich nieuniejętnych działań
Saizou :
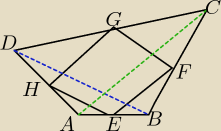
założenie: to rysunek
teza: środki boków dowolnego czworokąta są wierzchołkami równoległoboku
dowód:
Korzystam z tw. odwrotnego do Talesa, aby wykazać że odcinki lEHl i lBDl i lFGl są równoległe.
Korzystam z tw. odwrotnego do Talesa, aby wykazać że odcinki lGHl i lACl i lEFl są równoległe.
wiedząc że równoległobok ma dwie pary boków równoległych mogę stwierdzić, że
figura o wierzchołkach EFGH jest równoległobokiem
27 lip 17:14
Mila: Trochę inaczej
| CG | | CF | |
| =1= |
| ⇒GF||DB i ...? |
| GD | | FB | |
dalej ...
Teraz muszę przerwać pracę na forum.
27 lip 17:24
Saizou : a skąd mam wiedzieć że to jest równe 1 ?
27 lip 17:27
Krzychu: Bo punkt G jest w połowie odcinka DC
27 lip 17:29
27 lip 17:30
Krzychu: Polecenia: Wykaż, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku.
27 lip 17:31
Saizou : dziękuję
27 lip 17:31
Saizou : ja na teraz kończę i pojawię się jeszcze ok. 20, albo wcześniej
27 lip 17:36
Saizou : no i wróciłem
27 lip 19:15
Eta:
27 lip 19:17
Saizou : 1/ wykaż, że liczba 5
12−1 jest podzielna prze 21
2/ Wykaż,że liczba
√6−2
√5−
√5 jest całkowita
| | 1 | |
3/ Wiedząc,że liczba "a" jest rozwiązaniem równania x+ |
| =5 dla x≠0
|
| | x | |
| | 1 | |
Podaj wartość wyrażenia a3+ |
| , bez wyznaczania liczby "a" |
| | a3 | |
27 lip 19:18
Saizou : pozwoliłem sobie skopiować
1/
5
12−1=(5
6−1)(5
6+1)=(5
3+1)(5
3−1)(5
6+1)=126(5
3−1)(5
6+1)=7*18(5
3−1)(5
6+1)=7t , t∊C, bo
18(5
3−1)(5
6+1)∊C
27 lip 19:21
Eta:
Mogłeś bardziej wyeksponować
7*3*6(.......)
27 lip 19:31
rumpek: miałeś wykazać, że podzielne przez 21
więc: = 126(5
3 − 1)(5
6 + 1) =
21 * 6(5
3 − 1)(5
6 + 1) = 21 * t .. koniec
,
27 lip 19:32
Saizou : 2/ z naniesioną poprawką przy przepisywaniu
√6−2√5−√5=a a∊C
√6−2√5=a+√5
6−2√5=a2+2a√5+5
a2+2a√5−1+2√5=0
(a2−1)+2a√5+2√5=0
(a−1)(a+1)+2√5(a+1)=0
(a+1)(a−1+2√5)=0
a=−1 lub a=1−2√5
tylko nie wiem jak odrzucić opcję 1−2√5
27 lip 19:34
Saizou : a ja sobie ubzdurałem że podzielność przez 7
27 lip 19:35
nikt: a kolega nadal nie zna definicji pierwiastka arytmetycznego xD
Próbowałem wbić mu ją dwa dni temu ale mi nie wyszło
I'm no one
27 lip 19:36
rumpek: √6 − 2√5 −
√5 = (*) to jest wzór skróconego mnożenia
(*) =
√(√5 − 1)2 −
√5 =
= |
√5 − 1| −
√5 = dokończ sam
27 lip 19:36
Saizou : |√5 − 1| − √5=√5−1−√5=−1
27 lip 19:38
Eta:
27 lip 19:41
27 lip 19:43
nikt: Eta twoje zadania z poprzedniego postu to są tylko dla Saizou ?
27 lip 19:44
Saizou : 3/
| | 1 | | 1 | | 1 | |
a3+3a2* |
| +3a* |
| + |
| =125
|
| | a | | a | | a3 | |
27 lip 19:45
Eta:
Tak !
nikt inny nie może rozwiązywać
27 lip 19:46
Eta:
3/
27 lip 19:46
nikt: a nikt który nie jest inny może spróbować
27 lip 19:47
Eta:
27 lip 19:48
nikt: :(
27 lip 19:48
Eta:
Dla Ciebie zaraz napiszę specjalne zadanko
27 lip 19:49
nikt: już się boje
27 lip 19:49
Eta:
1/ Wykaż, że dla x,y,x, >0 zachodzi nierówność
27 lip 19:52
Saizou : to chyba nie było dla mnie zadanie
27 lip 19:55
nikt: Korzystam z tego że średnia arytmetyczna jest większa od średniej geometrycznej :
przemnażając obie strony nierówności przez 3 otrzymuję :
27 lip 19:56
nikt: c.n.w.
27 lip 19:56
Eta:
2/ Trójkąt ABC jest równoboczny. Punkty B,C,N są współliniowe.
Na boku AC wybrano taki punkt M taki,że |AM|= |C N|
Wykaż,że |BM|= |MN|
27 lip 19:57
nikt: To też dla mnie ?
27 lip 19:57
Eta:
Pięknie
.... nauka nie poszła w las
27 lip 19:58
Saizou : Eto dla kogo to zadanie?
27 lip 19:59
Eta:
Tak, dla Ciebie
Ulissesku
Saizou też może podać dowód
27 lip 19:59
Eta:
Ciekawe kto pierwszy poda poprawny dowód
27 lip 20:00
Eta:
3/ dla
Saizou ( i
Nikt
Wykaż,że punkt przecięcia przekątnych trapezu leży na prostej
przechodzącej przez środki jego podstaw
27 lip 20:04
Vax: W 3 można jeszcze pokazać, że na danej prostej leży również punkt przecięcia ramion trapezu.
27 lip 20:06
Eta:
4/ Na boku BC trójkąta ABC wybrano taki punkt P,że |∡CAP|= |∡ABC|,
Odcinek AF zawiera się w dwusiecznej kąta PAB
Wykaż,że |CE|= |AC|
27 lip 20:09
Eta:
Jasne,że można
dla
Vax
27 lip 20:11
Eta:
@
Nikt ........ i jak idzie? ........ cosik długawo
27 lip 20:13
nikt: Nie radzę sobie
Daj mi jeszcze tak z trzy godzinki i może będzie gotowe
27 lip 20:17
Vax: W 4 powinno być chyba dane, że odcinek AE zawiera się w dwusiecznej kąta PAB (a dokładnie E
należy do boku BC), gdyż teza zawiera jakiś punkt E, którego nie zawiera założenie
27 lip 20:18
Godzio: Nad
Etowymi zadankami można czasem siedzieć i siedzieć, nawet jeśli są super proste
27 lip 20:18
Krzychu: Eta: z jakiej ksiazki to czerpiesz?
27 lip 20:19
Eta:
Słuszna uwaga
Vax
zad4/ odcinek AE zawiera się ......
27 lip 20:22
Eta:
Godzio >...............
27 lip 20:23
Godzio:
Byłem na mini wakacjach, a tak to ciągle pracuje i śpię i nie mam czasu w ogóle żeby wejść na
dłużej na forum :<
27 lip 20:25
Eta:
@
Krzychu .......... z własnego
archiwum .... prawie jak w IPN
27 lip 20:25
Eta:
Hmmm
........ myślę,że na randki znajdujesz czas
27 lip 20:27
Eta:
Ostatni wpis do
Godzia.......... ma się rozumieć
27 lip 20:28
Godzio:
Oj, z tym też bywa ciężko, aczkolwiek czasami się zmuszę, a później nie żyje w pracy
27 lip 20:28
Eta:
Pracuj, pracuj
bo czekam,że odkupisz ........ mojego poczciwego "merola"
27 lip 20:30
Godzio: A teraz zbieram na mojego "mercedesa" więc duuuuuuużo pracuje
27 lip 20:31
Godzio:
Haha
, ale żeśmy się zgrali
(za pół darmo
)
27 lip 20:31
Eta:
27 lip 20:32
27 lip 20:33
Eta:
.... coś w tym jest ? no nie? ( to nie pierwszy raz)
27 lip 20:33
nikt: N może leżeć poza bokiem BC
27 lip 20:34
Vax: Spox
27 lip 20:36
Eta:
27 lip 20:39
Saizou : mam rozwiązanie do tego trójkąta, tylko niech mi się obrazek wczyta to wrzucę
27 lip 20:47
Eta:
Ok
27 lip 20:48
Saizou :
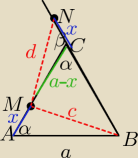
α=60
o
β=120
o
zatem z tw. Cosunusów wychodzi, że
c
2=x
2+a
2−xa
oraz że
| | 1 | |
d2=(a−x)2+x2−2(a−x)x*(− |
| )
|
| | 2 | |
d
2=a
2+x
2−ax
cnu
27 lip 20:49
Eta:
Podaj jeszcze inny sposób
27 lip 20:51
Saizou : a taki nie może być?
27 lip 20:52
nikt: Ja sie poddaje
To nie jest mój poziom
27 lip 20:54
Vax:
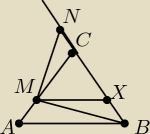
Można bez twierdzenia cosinusów. Weźmy taki punkt X, że BX = AM, wówczas MXC jest równoboczny,
więc ΔXMB == ΔCMN (bkb), skąd wynika teza.
27 lip 20:54
Eta:
No to jeszcze trzeci sposób
27 lip 20:56
Eta:
Ejj
Nikt vel
ICSP ............ poddajesz się?
27 lip 20:58
Eta:
Czekam na
trzeci sposób
27 lip 20:59
27 lip 21:04
Eta:
Nie!......... jeszcze inny sposób
27 lip 21:06
nikt: ICSP się poddał
27 lip 21:07
Eta:
Myśleć, myśleć
Podam ten dowód ..............za 2 godziny
27 lip 21:08
Eta:
Omg
......... dostanę zawału przez Ciebie
ICSP
27 lip 21:09
nikt: Jak widzisz mój nowy nick ma pokrycie w rzeczywistości
Wykładam się nawet na najprostszych zadaniach
27 lip 21:10
pigor: ... no to
zad.4. zgodnie z warunkami zadania :
|∡CAF|=|∡ABF|+|∡BAF|=|∡AFC| − jako kąt zewnętrzny
ΔABF nie przyległy do |∡ABF| ani |∡BAF|, zatem
ΔACF − równoramienny i
|CF|=AC| c.n.w. . ...
27 lip 21:40
Saizou : na dzisiaj koniec następne dowody na jutro zostawiam
27 lip 21:57
Eta:
Ok
Miłych snów
27 lip 22:04
pigor: ...
a zad. założenie: to rysunek , teza: środki boków dowolnego czworokąta są
wierzchołkami równoległoboku , to dowód np. tak :
GF∥BD i |GF|=
12|BD|
i ⇒ GE∥HE i |GF|=|HE| , zatem czworokąt EFGH − równoległobok c.n.w.
HE∥BD i |HE|=
12|BD|
27 lip 22:12
Saizou : jakaś podpowiedź do zadania z trapezem
28 lip 19:07
rumpek: Że to zadanie: Wykaż,że punkt przecięcia przekątnych trapezu leży na prostej przechodzącej
przez środki jego podstaw?
28 lip 19:22
Saizou :
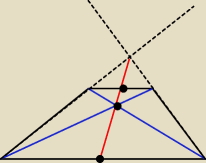
ale rysunek potrafię zrobić
28 lip 19:25
rumpek: no i masz o środkach wspomniane
więc tw. Talesa
28 lip 19:26
Eta:
28 lip 20:03
Saizou :
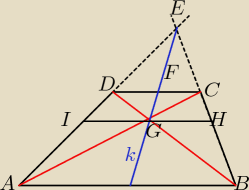
| EF | | EF | |
| = |
| , zatem odcinki lDEl i lCFl są sobie równe, wówczas prosta k dzieli każdą |
| DF | | CF | |
prostą równoległą do lDCl na dwie równe części. Punkt G, który znajduje się na tej prostej
dzieli odcinek lHIl na dwie równe częśći, zatem z warunków zadania wynika że punkt G to punkt
przecięcia się przekątnych trapezu ABCD, wówczas można stwierdzić, że dowód jest prawdziwy
cnu
28 lip 20:04
Saizou : *wówczas można stwierdzić, że teza jest prawdziwy
28 lip 20:08
Saizou : ktoś sprawdzi
28 lip 20:45
Vax: Ale opisz dokładnie, jak definiujesz prostą k, wierzchołki F,G itd (Np prostą k możesz
definiować jako prostą przechodzącą przez środki podstaw, albo prostą przechodzącą przez punkt
E i środek jednej podstawy itd, sposób definiowania ma duży wpływ na sposób dowodzenia).
28 lip 20:51
Saizou : to ja zrobię miks i napiszę prosta k to prosta przechodząca przez środki podstaw trapezu ABCD i
przez punkt E
28 lip 20:56
Vax: Ale nie możesz tego założyć, bo to masz wykazać.
28 lip 20:57
Saizou : a wierzchołki F, G to punkty przecięcia prostej k z odcinkami lCDl i lHIl
28 lip 20:58
28 lip 20:59
Saizou : a mnie miałem wykazać że punkt G leży na prostej k
28 lip 21:05
Vax: Miałeś, ale nie możesz założyć, że E i środki podstaw leżą na jednej prostej, gdyż w ogólności
przez dowolne 3 punkty nie zawsze przechodzi prosta, jeżeli chcesz z tego skorzystać musisz to
najpierw udowodnić
28 lip 21:09
Vax: ICSP już^^
28 lip 21:12
nikt: Dzięki
28 lip 21:28
Eta:
28 lip 21:32
Eta:
Tylko dla
Saizou
Zad 5/Pole trapezu jest równe
P, a stosunek długości podstaw trapezu wynosi
2.
Przekątne trapezu podzieliły ten trapez na cztery trójkąty. Wyznacz pole każdego z nich.
28 lip 21:40
Eta:
Zad. 6/ Punkt K leży na ramieniu BC trapezu ABCD , gdzie AB II BC.
Wykaż ,że |∡AKD|= |∡BAK|+ |∡CDK|
28 lip 21:44
Eta:
Zad.7 / Na okręgu o promieniu
r opisano trapez równoramienny, którego długość
jednej z podstaw wynosi
4r. Wyznacz odległość środka S tego okręgu
od każdego z wierzchołków trapezu.
Zadania ............. tylko dla
Saizou !
28 lip 21:49
rumpek:
28 lip 21:58
Saizou :
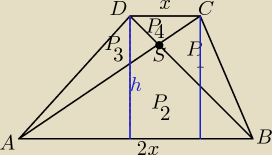
To najpierw wykaże, że P
1=P
3
ΔABD=ΔABC
bo wysokości h są opuszczone na podstawę 2x dla obu trójkątów
P
3+P
2=P
1+P
2
P
3=P
2
pole trapezu to P
t=P
1+p
2+P
3+P
4
P
t=2P
1+P
2+P
4
i dalej będę kombinować
28 lip 21:58
Eta:
Co
rumpek ? drugi raz będziesz zdawać maturę ?
28 lip 22:06
rumpek: teoretycznie sesje są jak matury
28 lip 22:08
Eta:
28 lip 22:11
28 lip 22:11
Eta:
28 lip 22:15
Eta:
@
rumpek
Pamiętasz moje ulubione wzorki? ( z zad.5)
28 lip 22:30
rumpek: tego się nie zapomina
28 lip 22:40
Saizou : zauważmy, że P
1 i P
2 są podobne (na zasadzie kbk) w skali 2, co więcej można pokazać że w
trójkątach ΔBSC i ΔABS stosunek długości podstaw, na którą jest opuszczona wysokość z
wierzchołka B , analogicznie możemy uzasadnić to dla pozostałych trójkątów, zatem
P=2P
2
P
1=2P=4P
2, wówczas pole trapezu to
P
t=P
2+4P
2+2P
2+2P
2=9P
2
zatem
a rysunek zaraz bo mi się nie wczytał
28 lip 22:44
Saizou :
28 lip 22:46
Eta:
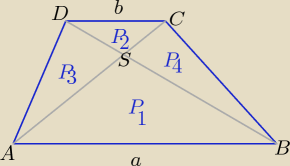
Ok
To teraz podam takie dwa wzorki ( możesz je z łatwością wykazać)
| | a | |
|
| = k −− skala podobieństwa ΔABS i DCS |
| | b | |
P(tr) = (k+1)
2*P
2 P
1= k
2*P
2 P
3=P
4= k*P
2
i drugi: P(tr)= P
1+ 2P
3+P
2 = (
√P1+
√P2)
2 , gdzie : P
3=P
4=
√P1*P2
28 lip 23:22
Eta:
@
Saizou dawaj zad.6/ i zad.7/
28 lip 23:27
Eta:
A może już za bardzo Cię zmęczyłam zad. 5/
28 lip 23:28
Saizou :
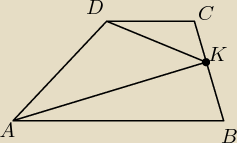
a w tym zad 6 musi być błąd
Punkt K leży na ramieniu BC trapezu ABCD , gdzie AB II BC. Wykaż ,że |∡AKD|= |∡BAK|+
|∡CDK|
patrząc na rysunek AB nie może być równoległe do BC, bo przecież BC to ramię, a AB podstawa
28 lip 23:32
Eta:
Sorry ( chochlik)
Ma być : AB II DC
28 lip 23:40
Saizou : może jakaś podpowiedź?
28 lip 23:58
Eta:
Ejjj tam
to banalny dowód......... pomyśl i 1 minuta na dowód wystarczy
29 lip 00:00
rumpek: jakby co, to chętnie
29 lip 00:03
Eta: 
29 lip 00:03
rumpek: 
29 lip 00:03
Eta:
29 lip 00:04
rumpek: 
29 lip 00:05
Eta:
29 lip 00:07
rumpek: ok, to może coś łatwego dla
Saizou
zad.9 / Wykaż że każda liczba postaci 10
n+2 gdzie n∈ N⁺ jest podzielna przez 3.
29 lip 00:09
Saizou :
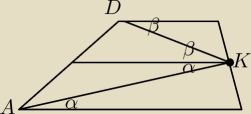
to na mocy kątów odpowiadających i naprzemianległych mamy ∡AKD=α+β
cnu
29 lip 00:10
Eta:
29 lip 00:10
Eta:
Superr
(i co?.... 1 min wystarczyła?
29 lip 00:11
Saizou : dla dowolnego n∊N liczba 10n=10*10*10...10, zatem suma cyfr tej liczby będzie równa 1, jeśli
dodamy jeszcze do niej 2 to suma cyfr tej liczby będzie równa 3. Liczba jest podzielna przez 3
gdy suma jej cyfr jest podzielna przez 3 cnu
29 lip 00:13
rumpek: pisałem, że łatwe
to teraz dokończ to zadanie 5 od
Ety
29 lip 00:14
Eta:
29 lip 00:14
Eta:
Zostało jeszcze zad.7
29 lip 00:17
Mila: Podziwiam, podziwiam, dobranoc uczącym i Saizou.
29 lip 00:23
Eta:
K o l o r o w y c h snów
Milu
29 lip 00:26
Saizou :
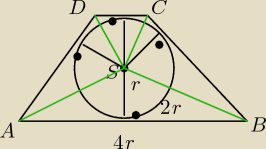
do wierzchołka B i A bo te odległości będą równe
r
2+4r
2=BS
2
5r
2=BS
2
r
√5=BS=AS
29 lip 00:28
Eta:
Jeszcze |SC|= |SD|= ?
29 lip 00:29
Mila: Wzajemnie
Dla wszystkich.
29 lip 00:29
Saizou : właśnie
Mila śpij dobrze, aby mieć cierpliwość dla mnie
29 lip 00:32
Eta:
29 lip 00:33
rumpek: To co
Saizou za 2 miesiące zaczynamy całeczki
?
29 lip 00:35
Eta:
I zmawiaj na razie .... pacierze, bo będą też .... macierze
29 lip 00:38
29 lip 00:39
rumpek: "kto liczy całeczki ten ma fajne
... "
[... − odpowiednie uzupełnić]
29 lip 00:40
Eta:
Pora na spanie
Dobranoc Wszystkim
29 lip 00:53
Saizou : Dobranoc Eta miłych snów
29 lip 00:54
Saizou : dzisiaj rano dokończę i teraz idę spać < miłych snów>
29 lip 01:00
Saizou :
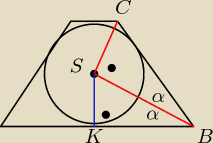
zauważmy, że trójkąty ΔSBK i ΔBCS są podobne, zatem możemy zapisać:
r
2√5=2r*lCSl
29 lip 11:07
pigor: ...
nieprawda
29 lip 13:02
