Gustlik:
To wynika z polowej metody wyznaczania drogi, a dokładniej z rachunku całkowego i
różniczkowego, ale pewnie tego nie znasz, więc nie będę tego na razie wyprowadzał.
Niemniej warto wiedzieć, że droga jest zawsze równa polu figury powstałej pod wykresem
zależności prędkości od czasu v=v(t).
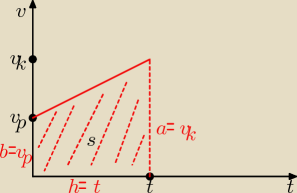
Dla ruchu jednostajnie przyśpieszonego/opóźnionego jest to trapez − patrz rysunek.
Pole trapezu
Z rysunku widać, że a=v
k, b=v
p, h=t, P=s
Podstawiając do (1) mamy:
Dla dowolnego rodzaju ruchu prawdziwy jest wzór na prędkość średnią:
| | s | |
vśr= |
| , stąd s=vśr*t (3) |
| | t | |
Porównując (3) z (*2) mamy wzór na prędkość średnią dla ruchu jednostajnie
przyśpieszonego/opóźnionego, czyli jednostajnie zmiennego:
Czyli prędkość średnia w tym ruchu jest równa średniej arytmetycznej prędkości początkowej i
końcowej.
Wzór ten pozwala na ominięcie skomplikowanego i niestety jak każda skomplikowana metoda −
ukochanego przez nauczycieli wzoru na drogę w ruchu jednostajnie zmiennym
Szczerze mówiąc ja unikam tego wzoru jak ognia, wymaga on często skomplikowanych i żmudnych
obliczeń, układów równań 2 stopnia, zwłaszcza jak mamy dane np. dwie prędkości i drogę, a
wyjątkowo rzadko jest on potrzebny.
Zamiast stosować ten koszmarny wzór wystarczy obliczyć prędkość średnią:
i potem drogę lub czas ze wzoru
s=v
śr*t i po kłopocie.
Jest jeszcze jeden fajny wzorek na ruch jednostajnie zmienny − tzw. wzór bezczasowy:
v
k2−v
p2=2as (6)
UWAGA
! w ruchu jednostajnie opóźnionym przy korzystaniu z tego wzoru trzeba przyjąć ujemne
przyśpieszenie
!
Wyprowadzenie:
v
k2−v
p2=(v
k−v
p)(v
k+v
p)
ale:
v
k−v
p=Δv=at
stąd:
| | s | |
vk2−vp2=(vk−vp)(vk+vp)=at*2* |
| =2as , bo czas się skraca. |
| | t | |
Ten wzór bezczasowy to drogi sposób na ominięcie tego koszmarnego wzoru na drogę (5). Możemy go
stosować, gdy w zadaniu mamy podane dwie prędkości i drogę − wtedy obliczymy przyspieszenie
albo dwie prędkości i przyśpieszenie − wtedy obliczymy drogę.
Zdarzają się też zadania, że przydają się oba wzory − i prędkość średnia (4) i bezczasowy (6).
